【题目】“科技引领，布局未来”科技研发是企业发展的驱动力量。
年，某企业连续
年累计研发投入搭
亿元，我们将研发投入与经营投入的比值记为研发投入占营收比，这年间的研发投入（单位：十亿元）用右图中的折现图表示，根据折线图和条形图，下列结论错误的使（ ）
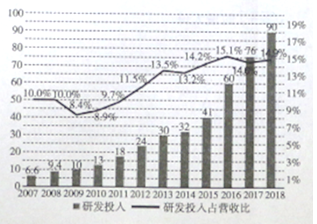
A. 
年至
年研发投入占营收比增量相比
年至
年增量大
B. 年至
年研发投入增量相比
年至
年增量小
C. 该企业连续年研发投入逐年增加
D. 该企业来连续年来研发投入占营收比逐年增加
开心练习课课练与单元检测系列答案科目：高中数学 来源： 题型：
【题目】（1）已知两个变量线性相关，若它们的相关性越强，则相关系数的绝对值越接近于1.
（2）线性回归直线必过点
；
（3）对于分类变量A与B的随机变量
，越大说明“A与B有关系”的可信度越大.
（4）在刻画回归模型的拟合效果时，残差平方和越小，相关指数
的值越大，说明拟合的效果越好.
（5）根据最小二乘法由一组样本点
，求得的回归方程是
，对所有的解释变量
,
的值一定与
有误差.
以上命题正确的序号为____________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知椭圆
，直线
，直线
与椭圆
交于不同的两点
，点
和点
关于
轴对称，直线
与轴交于点
．
（1）若点
是椭圆的一个焦点，求该椭圆的长轴的长度；
（2）若
，且
，求
的值；
（3）若
，求证：
为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店刚刚上市了《中国古代数学史》，销售前该书店拟定了5种单价进行试销，每本单价（
元）试销l天，得到如表单价（元）与销量
（册）数据：
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
（1）已知销量与单价具有线性相关关系，求
关于的线性回归方程；
（2）若该书每本的成本为
元，要使得售卖时利润最大，请利用所求的线性相关关系确定单价应该定为多少元？（结果保留到整数）
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：
，
．
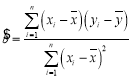
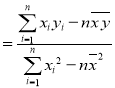查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线l1：kx-y+4=0与直线l2：x+ky-3=0相交于点P，则当实数k变化时，点P到直线4x-3y+10=0的距离的最大值为（ ）
A.2B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》是中国古代第一部数学专著，全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中，原文记载如下：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。”其核心思想编译成如示框图，若输入的
，
分别为45，63，则输出的为（ ）
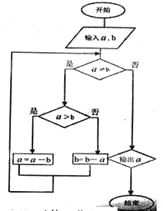
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在教材中，我们已研究出如下结论：平面内
条直线最多可将平面分成
个部分．现探究：空间内个平面最多可将空间分成多少个部分，
．设空间内个平面最多可将空间分成
个部分．
（1）求
的值；
（2）用数学归纳法证明此结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
