
【题目】已知圆![]() .由直线
.由直线![]() 上离圆心最近的点
上离圆心最近的点![]() 向圆
向圆![]() 引切线,切点为
引切线,切点为![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】圆心![]() 到直线
到直线![]() 的距离:
的距离:![]() ,
,
结合几何关系可得线段![]() 的长度为
的长度为![]() .
.
【题型】填空题
【结束】
16
【题目】设![]() 是两个非零平面向量,则有:
是两个非零平面向量,则有:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]()
④若存在实数![]() ,使得
,使得![]() ,则
,则![]() 或
或![]() 四个命题中真命题的序号为 __________.(填写所有真命题的序号)
四个命题中真命题的序号为 __________.(填写所有真命题的序号)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
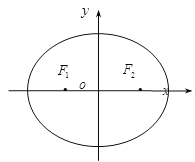
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() (
(![]() ,
,![]() ),且两个焦点
),且两个焦点![]() ,
,![]() 的坐标依次为(
的坐标依次为(![]() 1,0)和(1,0).
1,0)和(1,0).
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求当
,求当![]() 为何值时,直线
为何值时,直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)设数列![]() 满足
满足![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:
(1)由题意结合三角形内角和为![]() 可得
可得![]() .由余弦定理可得
.由余弦定理可得![]() ,,结合勾股定理可知
,,结合勾股定理可知![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)结合(1)中的结论可得![]()
![]() .则
.则![]()
![]() ,
,![]() 据此可得关于实数k的方程
据此可得关于实数k的方程![]() ,解方程可得
,解方程可得![]() ,则
,则![]() 或
或![]() .
.
试题解析:
(1)由已知![]() ,又
,又![]() ,所以
,所以![]() .又由
.又由![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
(2)![]()
![]() .
.
所以![]()
![]()
![]() ,
,![]() 由
由![]() ,得
,得
![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() .
.
【题型】解答题
【结束】
18
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)由题意可得圆的一条直径所在的直线方程为![]() ,据此可得圆心
,据此可得圆心![]() ,半径
,半径![]() ,则所求圆的方程为
,则所求圆的方程为![]() .
.
(2)圆的标准方程为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,两圆连心线斜率
,两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,结合弦长公式可得
,结合弦长公式可得![]() ,
,![]() .则圆的方程为
.则圆的方程为![]() .
.
试题解析:
(1)过点![]() 且与直线
且与直线![]() 垂直的直线为
垂直的直线为![]() ,
,
由![]()
![]() .
.
即圆心![]() ,半径
,半径![]() ,
,
所求圆的方程为![]() .
.
(2)圆方程化为![]() ,得该圆圆心为
,得该圆圆心为![]() ,半径为
,半径为![]() ,故两圆连心线斜率
,故两圆连心线斜率![]() .设所求圆心为
.设所求圆心为![]() ,
,
![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
∴![]() .
.
点睛:求圆的方程,主要有两种方法:
(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.
(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式.
【题型】解答题
【结束】
20
【题目】如图所示,![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com