
已知P(x,y),A(-1,0),向量 与
与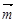 =(1,1)共线。
=(1,1)共线。
(1)求y关于x的函数解析式;
(2)是否在直线y=2x和直线y=3x上分别存在一点B、C,使得满足∠BPC为锐角时x取值集合为{x| x<-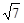 或x>
或x>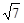 }?若存在,求出这样的B、C的坐标;若不存在,说明理由。
}?若存在,求出这样的B、C的坐标;若不存在,说明理由。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
梯形ABCD中,AB∥CD,AB=2CD,M、N分别是CD和AB的中点,若 =a,
=a, =b,试用a、b表示
=b,试用a、b表示 和
和 ,则
,则 =________,
=________, =______.
=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com