
【题目】已知函数f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若x∈[0, ![]() ],求函数f(x)的最值及相应x的取值.
],求函数f(x)的最值及相应x的取值.
【答案】解:(Ⅰ)f(x)=sin2x+2sinxcosx+3cos2x=sin2x+2cos2x+1 =sin2x+cos2x+2= ![]() sin(2x+
sin(2x+ ![]() )+2,
)+2,
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
则kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
则有函数的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
(Ⅱ)当x∈[0, ![]() ]时,2x+
]时,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
则有sin(2x+ ![]() )∈[﹣1,1],
)∈[﹣1,1],
则当x= ![]() 时,f(x)取得最小值,且为1,
时,f(x)取得最小值,且为1,
当x= ![]() 时,f(x)取得最大值,且为
时,f(x)取得最大值,且为 ![]() +2
+2
【解析】(Ⅰ)运用二倍角的正弦和余弦公式,及两角和的正弦公式,化简函数f(x),再由正弦函数的周期和单调增区间,解不等式即可得到.(Ⅱ)由x的范围,可得2x﹣2x+ ![]() 的范围,再由正弦函数的图象和性质,即可得到最值.
的范围,再由正弦函数的图象和性质,即可得到最值.
【考点精析】解答此题的关键在于理解正弦函数的单调性的相关知识,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数,以及对三角函数的最值的理解,了解函数
上是减函数,以及对三角函数的最值的理解,了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】如果数列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),满足:①
),满足:①![]() ,
,![]() ;
;
②![]() ,那么称数列
,那么称数列![]() 为“
为“![]() ”数列.
”数列.
(![]() )已知数列
)已知数列![]() ,
,![]() ,
,![]() ,
,![]() ;数列
;数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试判断数列
.试判断数列![]() ,
,![]() 是否为“
是否为“![]() ”数列.
”数列.
(![]() )是否存在一个等差数列是“
)是否存在一个等差数列是“![]() ”数列?请证明你的结论.
”数列?请证明你的结论.
(![]() )如果数列
)如果数列![]() 是“
是“![]() ”数列,求证:数列
”数列,求证:数列![]() 中必定存在若干项之和为
中必定存在若干项之和为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.

(1)求![]() 的值;
的值;
(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
x2﹣lnx在其定义域的一个子区间(k﹣1,k+1)上不是单调函数,则实数k的取值范围是( )
A.(1,2)
B.[1,2)
C.[0,2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=![]() .
.
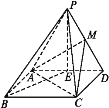
(1)求证:PB∥平面MAC.
(2)求证:平面MAC⊥平面PBE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了加强环保建设,提高社会效益和经济效益,某市计划用若干年时间更换一万辆燃油型公交车。每更换一辆新车,则淘汰一辆旧车,更换的新车为电力型车和混合动力型车。今年初投入了电力型公交车![]() 辆,混合动力型公交车
辆,混合动力型公交车![]() 辆,计划以后电力型车每年的投入量比上一年增加
辆,计划以后电力型车每年的投入量比上一年增加![]() ,混合动力型车每年比上一年多投入
,混合动力型车每年比上一年多投入![]() 辆.设
辆.设![]() 、
、![]() 分别为第
分别为第![]() 年投入的电力型公交车、混合动力型公交车的数量,设
年投入的电力型公交车、混合动力型公交车的数量,设![]() 、
、![]() 分别为
分别为![]() 年里投入的电力型公交车、混合动力型公交车的总数量。
年里投入的电力型公交车、混合动力型公交车的总数量。
(1)求![]() 、
、![]() ,并求
,并求![]() 年里投入的所有新公交车的总数
年里投入的所有新公交车的总数![]() ;
;
(2)该市计划用![]() 年的时间完成全部更换,求
年的时间完成全部更换,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AA1=2,AC= ![]() ,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( )
,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率;
的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com