
°ĺŐ‚ńŅ°Ņő™Ņľ≤žłŖ÷–…ķĶń–‘Īū”Ž «∑ŮŌ≤Ľ∂ ż—ßŅő≥Ő÷ģľšĶńĻōŌĶ£¨‘ŕń≥≥« –Ķńń≥–£łŖ÷–…ķ÷–£¨ī”ń–…ķ÷–ňśĽķ≥ť»°Ńň70»ň£¨ī”Ňģ…ķ÷–ňśĽķ≥ť»°Ńň50»ň£¨ń–…ķ÷–Ō≤Ľ∂ ż—ßŅő≥ŐĶń’ľ![]() £¨Ňģ…ķ÷–Ō≤Ľ∂ ż—ßŅő≥ŐĶń’ľ
£¨Ňģ…ķ÷–Ō≤Ľ∂ ż—ßŅő≥ŐĶń’ľ![]() £¨Ķ√ĶĹ»ÁŌ¬Ń–Ń™ĪŪ.
£¨Ķ√ĶĹ»ÁŌ¬Ń–Ń™ĪŪ.
Ō≤Ľ∂ ż—ßŅő≥Ő | ≤ĽŌ≤Ľ∂ ż—ßŅő≥Ő | ļŌľ∆ | |
ń–…ķ | |||
Ňģ…ķ | |||
ļŌľ∆ |
£®1£©«ŽĹęŃ–Ń™ĪŪ≤Ļ≥šÕÍ’Ż£Ľ ‘Ň–∂Ōń‹∑Ů”–90%Ķńį—ő’»Ōő™Ō≤Ľ∂ ż—ßŅő≥Ő”Ž∑Ů”Ž–‘Īū”–Ļō£Ľ
£®2£©ī”≤ĽŌ≤Ľ∂ ż—ßŅő≥ŐĶń—ß…ķ÷–≤…”√∑÷≤„≥ť—ýĶń∑Ĺ∑®£¨ňśĽķ≥ť»°6»ň£¨Ō÷ī”6»ň÷–ňśĽķ≥ť»°2»ň£¨«ů≥ť»°Ķń—ß…ķ÷–÷Ń…Ŕ”–1√Ż «Ňģ…ķĶńłŇ¬ ..
łĹ£ļ![]() £¨∆š÷–
£¨∆š÷–![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£¨√Ľ”–![]() Ķńį—ő’£®2£©
Ķńį—ő’£®2£©![]()
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©Ĺę żĺ›īķ»ŽŅ®∑ĹĻę Ĺ«ůĶ√![]() £¨‘Ŕ∂‘’’≤őŅľ żĺ›Ķ√ĹŠ¬Ř£®2£©Ō»łýĺ›∑÷≤„≥ť—ý»∑∂®≥ť»°ń–…ķŇģ…ķ»ň ż£¨‘ŔņŻ”√√∂ĺŔ∑®»∑∂®ī”6»ň÷–ňśĽķ≥ť»°2»ň◊‹ ¬ľĢ ż£¨ī”÷–»∑∂®÷Ń…Ŕ”–1√Ż «Ňģ…ķ ¬ľĢ ż£¨◊Óļůłýĺ›ĻŇĶšłŇ–ÕłŇ¬ Ļę Ĺ«ůłŇ¬
£¨‘Ŕ∂‘’’≤őŅľ żĺ›Ķ√ĹŠ¬Ř£®2£©Ō»łýĺ›∑÷≤„≥ť—ý»∑∂®≥ť»°ń–…ķŇģ…ķ»ň ż£¨‘ŔņŻ”√√∂ĺŔ∑®»∑∂®ī”6»ň÷–ňśĽķ≥ť»°2»ň◊‹ ¬ľĢ ż£¨ī”÷–»∑∂®÷Ń…Ŕ”–1√Ż «Ňģ…ķ ¬ľĢ ż£¨◊Óļůłýĺ›ĻŇĶšłŇ–ÕłŇ¬ Ļę Ĺ«ůłŇ¬
‘Ő‚Ĺ‚őŲ£ļĹ‚£ļ£®ĘŮ£©![]() Ń–Ń™ĪŪ≤Ļ≥š»ÁŌ¬£ļ
Ń–Ń™ĪŪ≤Ļ≥š»ÁŌ¬£ļ
Ō≤Ľ∂ ż—ßŅő≥Ő | ≤ĽŌ≤Ľ∂ ż—ßŅő≥Ő | ļŌľ∆ | |
ń–…ķ |
|
|
|
Ňģ…ķ |
|
|
|
ļŌľ∆ |
|
|
|
”…Ő‚“‚Ķ√![]() £¨
£¨
°Ŗ![]() £¨°ŗ√Ľ”–
£¨°ŗ√Ľ”–![]() Ķńį—ő’»Ōő™Ō≤Ľ∂ ż—ßŅő≥Ő”Ž∑Ů”Ž–‘Īū”–Ļō£ģ£©
Ķńį—ő’»Ōő™Ō≤Ľ∂ ż—ßŅő≥Ő”Ž∑Ů”Ž–‘Īū”–Ļō£ģ£©
£®ĘÚ£©”√∑÷≤„≥ť—ýĶń∑Ĺ∑®≥ť»° Ī£¨≥ť»°Ī»ņż «![]() £¨
£¨
‘Ú≥ť»°ń–…ķ![]() »ň£¨≥ť»°Ňģ…ķ
»ň£¨≥ť»°Ňģ…ķ![]() »ň£ģ
»ň£ģ
ľ«≥ť»°ĶńŇģ…ķő™![]() £¨≥ť»°Ķńń–…ķő™
£¨≥ť»°Ķńń–…ķő™![]() £¨
£¨
ī”÷–ňśĽķ≥ť»°![]() √Ż—ß…ķĻ≤”–
√Ż—ß…ķĻ≤”–![]() ÷÷«ťŅŲ£ļ
÷÷«ťŅŲ£ļ
![]()
![]() £ģ
£ģ
∆š÷–÷Ń…Ŕ”–![]() √Ż «Ňģ…ķĶń ¬ľĢő™£ļ
√Ż «Ňģ…ķĶń ¬ľĢő™£ļ
![]() ”–
”–![]() ÷÷«ťŅŲ£ģ
÷÷«ťŅŲ£ģ
ľ«°į≥ť»°Ķń—ß…ķ÷–÷Ń…Ŕ”–![]() √Ż «Ňģ…ķ°Īő™ ¬ľĢ
√Ż «Ňģ…ķ°Īő™ ¬ľĢ![]() £¨‘Ú
£¨‘Ú![]() £ģ
£ģ


 ‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©=sin ![]() +e©Ā|x©Ā1| £¨ ”–Ō¬Ń–ňńłŲĹŠ¬Ř£ļ
+e©Ā|x©Ā1| £¨ ”–Ō¬Ń–ňńłŲĹŠ¬Ř£ļ
ĘŔÕľŌůĻō”ŕ÷ĪŌŖx=1∂‘≥∆£Ľ
Ęŕf£®x£©Ķń◊Óīů÷Ķ «2£Ľ
ĘŘf£®x£©Ķń◊Óīů÷Ķ «©Ā1£¨£Ľ
Ę‹f£®x£©‘ŕ«Ýľš[©Ā2015£¨2015]…Ō”–2015łŲŃ„Ķ„£ģ
∆š÷–’ż»∑ĶńĹŠ¬Ř «£®–ī≥Ųňý”–’ż»∑ĶńĹŠ¬Ř–ÚļŇ£©£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕĪŖ≥§ő™4ĶńŃ‚–ő![]() ÷–£¨
÷–£¨ ![]() £¨Ķ„
£¨Ķ„![]() °Ę
°Ę![]() ∑÷Īū‘ŕĪŖ
∑÷Īū‘ŕĪŖ![]() °Ę
°Ę![]() …Ō£ģĶ„
…Ō£ģĶ„![]() ”ŽĶ„
”ŽĶ„![]() °Ę
°Ę![]() ≤Ľ÷ōļŌ£¨
≤Ľ÷ōļŌ£¨ ![]() £¨
£¨ ![]() £¨—ō
£¨—ō![]() Ĺę
Ĺę![]() ∑≠’ŘĶĹ
∑≠’ŘĶĹ![]() ĶńőĽ÷√£¨ Ļ∆Ĺ√ś
ĶńőĽ÷√£¨ Ļ∆Ĺ√ś![]() ∆Ĺ√ś
∆Ĺ√ś![]() £ģ
£ģ

£®ĘŮ£©«ů÷§£ļ ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®ĘÚ£©ľ«»żņ‚◊∂![]() ĶńŐŚĽżő™
ĶńŐŚĽżő™![]() £¨ňńņ‚◊∂
£¨ňńņ‚◊∂![]() ĶńŐŚĽżő™
ĶńŐŚĽżő™![]() £¨«“
£¨«“![]() £¨«ůīň ĪŌŖ∂ő
£¨«ůīň ĪŌŖ∂ő![]() Ķń≥§£ģ
Ķń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Ķ„![]() ő™‘≤
ő™‘≤![]() …Ō“Ľ∂ĮĶ„£¨
…Ō“Ľ∂ĮĶ„£¨![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() £¨»Ű∂ĮĶ„
£¨»Ű∂ĮĶ„![]() ¬ķ◊„
¬ķ◊„![]() £®∆š÷–
£®∆š÷–![]() ő™∑«Ń„≥£ ż£©
ő™∑«Ń„≥£ ż£©
£®1£©«ů∂ĮĶ„![]() ĶńĻžľ£∑Ĺ≥Ő£Ľ
ĶńĻžľ£∑Ĺ≥Ő£Ľ
£®2£©ĶĪ![]() Ī£¨Ķ√ĶĹ∂ĮĶ„
Ī£¨Ķ√ĶĹ∂ĮĶ„![]() ĶńĻžľ£ő™«ķŌŖ
ĶńĻžľ£ő™«ķŌŖ![]() £¨–Ī¬ ő™
£¨–Ī¬ ő™![]() 1Ķń÷ĪŌŖ
1Ķń÷ĪŌŖ![]() ”Ž«ķŌŖ
”Ž«ķŌŖ![]() ŌŗĹĽ”ŕ
ŌŗĹĽ”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨«ů
ŃĹĶ„£¨«ů![]() √śĽżĶń◊Óīů÷Ķ.
√śĽżĶń◊Óīů÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™’żŌÓ żŃ–{an}¬ķ◊„a1=1£¨£®n+1£©a2n+1+an+1an©Āna ![]() =0£¨ żŃ–{bn}Ķń«įnŌÓļÕő™Sn«“Sn=1©Ābn £ģ
=0£¨ żŃ–{bn}Ķń«įnŌÓļÕő™Sn«“Sn=1©Ābn £ģ
£®1£©«ů{an}ļÕ{bn}ĶńÕ®ŌÓ£Ľ
£®2£©ŃÓcn= ![]() £¨ ĘŔ«ů{cn}Ķń«įnŌÓļÕTn£Ľ
£¨ ĘŔ«ů{cn}Ķń«įnŌÓļÕTn£Ľ
Ęŕ «∑Ůīś‘ŕ’ż’Ż żm¬ķ◊„m£ĺ3£¨c2 £¨ c3 £¨ cm≥…Ķ»≤Ó żŃ–£Ņ»Űīś‘ŕ£¨«Ž«ů≥Ųm£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©=cosx+ax2©Ā1£¨a° R£ģ
£®1£©ĶĪa=0 Ī£¨«ůļĮ żf£®x£©‘ŕ ![]() ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£®2£©ĶĪa=1 Ī£¨«ůļĮ żf£®x£©‘ŕ[©Ā¶–£¨¶–]…ŌĶń◊Óīů÷ĶļÕ◊Ó–°÷Ķ£Ľ
£®3£©»Ű∂‘”ŕ»ő“‚Ķń Ķ żxļ„”–f£®x£©°›0£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™°ųABCĶń»żłŲńŕĹ«A£¨B£¨Cňý∂‘ĶńĪŖ∑÷Īūő™a£¨b£¨c£¨ŌÚŃŅ ![]() =£®c+a£¨b£©£¨
=£®c+a£¨b£©£¨ ![]() =£®c©Āa£¨b©Āc£©£¨«“
=£®c©Āa£¨b©Āc£©£¨«“ ![]() °Õ
°Õ ![]() £ģ
£ģ
£®1£©«ůĹ«AĶńīů–°£Ľ
£®2£©»Űa=3£¨«ů°ųABC÷‹≥§Ķń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ŌÚŃŅ ![]() ļÕ
ļÕ ![]() £¨∆š÷–
£¨∆š÷– ![]() £¨
£¨ ![]() £¨k° R£ģ
£¨k° R£ģ
£®1£©ĶĪkő™ļő÷Ķ Ī£¨”– ![]() °ő
°ő ![]() £Ľ
£Ľ
£®2£©»ŰŌÚŃŅ ![]() ”Ž
”Ž ![]() Ķńľ–Ĺ«ő™∂ŘĹ«£¨«ů Ķ żkĶń»°÷Ķ∑∂őߣģ
Ķńľ–Ĺ«ő™∂ŘĹ«£¨«ů Ķ żkĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨“—÷™’ż∑Ĺ–őABCDĶńĪŖ≥§ő™6£¨Ķ„E£¨F∑÷Īū‘ŕĪŖAB£¨AD…Ō£¨AE=AF=4£¨Ō÷Ĺę°ųAEF—ōŌŖ∂őEF’Ř∆ūĶĹ°ųA°šEFőĽ÷√£¨ ĻĶ√A°šC=2 ![]() £ģ
£ģ 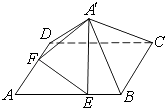
£®1£©«ůőŚņ‚◊∂A°š©ĀBCDFEĶńŐŚĽż£Ľ
£®2£©«ů∆Ĺ√śA°šEF”Ž∆Ĺ√śA°šBCĶńľ–Ĺ«£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com