
分析 (1)由题意知|PA1|,|A1A2|,|PA2|成等差数列.可得4a=a+4+|a-4|,解得a.又$\frac{1}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,a2=b2+c2,联立解出即可得出.
(2)假设存在.设M(x1,y1),N(x2,y2).当直线斜率存在且不为0时,设直线方程为y=kx+m.与椭圆方程联立化简得(4k2+1)x2+8kmx+4m2-4=0.因为过椭圆内的点,故此方程必有两根.利用根与系数的关系与数量积运算性质可得5m2+32km+12k2=0.解出并且验证即可得出.
解答 解:(1)由题意知,|PA1|=a+4,|A1A2|=2a,|PA2|=|a-4|,∵|PA1|,|A1A2|,|PA2|成等差数列.∴4a=a+4+|a-4|,解得a=2或0(舍去).又$\frac{1}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,a2=b2+c2,
联立解得b=1,c=$\sqrt{3}$.
故椭圆标准方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)假设存在.设M(x1,y1),N(x2,y2).
当直线斜率存在且不为0时,设直线方程为y=kx+m.
联立$\left\{\begin{array}{l}{{x}^{2}+4{y}^{2}=4}\\{y=kx+m}\end{array}\right.$,化简得(4k2+1)x2+8kmx+4m2-4=0.
因为过椭圆内的点,故此方程必有两根.
∴x1+x2=$\frac{-8km}{4{k}^{2}+1}$,x1•x2=$\frac{4{m}^{2}-4}{4{k}^{2}+1}$,
∴$\overrightarrow{PM}$•$\overrightarrow{PN}$=12=(x1-4)(x2-4)+y1y2
=(1+k2)x1•x2+(km-4)(x1+x2)+16+m2
=(1+k2)•$\frac{4{m}^{2}-4}{4{k}^{2}+1}$+(km-4)$\frac{-8km}{4{k}^{2}+1}$,x1+16+m2
=$\frac{60{k}^{2}+5{m}^{2}+32km+12}{4{k}^{2}+1}$,
故得5m2+32km+12k2=0.
∵k≠0,故有$5(\frac{m}{k})^{2}$+32$•\frac{m}{k}$+12=0,
解得m=-$\frac{2}{5}$k或m=-6k,
故直线方程为y=kx-$\frac{2}{5}$k或y=kx-6k.
则直线恒过点$(\frac{2}{5},0)$或(6,0),
因为此点在椭圆内部,故唯有点$(\frac{2}{5},0)$满足要求.
当直线斜率为0时,过点$(\frac{2}{5},0)$的直线与椭圆的交点显然即为M,N,$\overrightarrow{PM}$•$\overrightarrow{PN}$=(-6)×(-2)=12,满足.
当直线斜率不存在时,
过点$(\frac{2}{5},0)$的直线与椭圆的交点M,N为$(\frac{2}{5},\frac{2\sqrt{6}}{5})$,$(\frac{2}{5},-\frac{2\sqrt{6}}{5})$.
$\overrightarrow{PM}$•$\overrightarrow{PN}$=$(\frac{2}{5}-4)^{2}$-$(\frac{2\sqrt{6}}{5})^{2}$=12,亦满足.
综上,在椭圆内部存在点$(\frac{2}{5},0)$满足题目要求.
点评 本题考查了题意的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、数量积运算性质、分类讨论方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | $\{x|\frac{1}{2}<x≤1\}$ | C. | {x|x<1} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.
已知函数f(x)=sin(ωx-$\frac{π}{4}$)(ω>0,x∈R)的最小正周期为x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
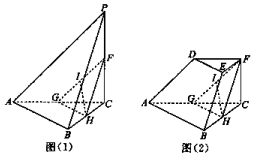 如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.
如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com