
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
【答案】
(1)解:因为f(x)是奇函数,所以f(0)=0 ![]() =0,解得b=1,
=0,解得b=1,
f(x)= ![]() ,又由f(1)=﹣f(﹣1)
,又由f(1)=﹣f(﹣1) ![]() ,解得a=2
,解得a=2
(2)证明:由(1)可得:f(x)= ![]() =
= ![]() .
.
x1<x2,∴ ![]() >0,
>0,
则f(x1)﹣f(x2)= ![]() =
= ![]() >0,
>0,
∴f(x1)>f(x2).
∴f(x)在R上是减函数
(3)解:∵函数f(x)是奇函数.
∴f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x)成立,
∵f(x)在R上是减函数,∴kx2<1﹣2x,
∴对于任意 ![]() 都有kx2<1﹣2x成立,
都有kx2<1﹣2x成立,
∴对于任意 ![]() 都有k<
都有k< ![]() ,
,
设g(x)= ![]() ,
,
∴g(x)= ![]() =
= ![]() ,
,
令t= ![]() ,t∈[
,t∈[ ![]() ,2],
,2],
则有 ![]() ,∴g(x)min=g(t)min=g(1)=﹣1
,∴g(x)min=g(t)min=g(1)=﹣1
∴k<﹣1,即k的取值范围为(﹣∞,﹣1)
【解析】(1)直接根据函数是奇函数,满足f(﹣x)=﹣f(x),把x=0,和x=1代入,即可得到关于a,b的两个等式,解方程组求出a,b的值.(2)利用减函数的定义即可证明.(3)f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x),即k< ![]() 成立,设g(x)=
成立,设g(x)= ![]() ,
,
换元使之成为二次函数,再求最小值.
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x﹣a|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)不等式f(x)<4的解集中的整数有且仅有1,2,3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点在抛物线
的焦点在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(Ⅰ)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过点![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线, ![]() 、
、![]() 分别为两个切点,求
分别为两个切点,求![]() 面积的最小值.
面积的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1:y=a和l2:y= ![]() (其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4
(其中a>0),若直线l1与函数y=|log4x|的图象从左到右相交于点A,B,直线l2与函数y=|log4x|的图象从左到右相交于点C,D.记线段AC和BD在x轴上的投影长度分别为 m,n.令f(a)=log4 ![]() .
.
(1)求f(a)的表达式;
(2)当a变化时,求出f(a)的最小值,并指出取得最小值时对应的a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga(1﹣x)(a>0且a≠1).
(1)求f(x)+g(x)的定义域;
(2)判断函数f(x)+g(x)的奇偶性,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一根水平放置的长方体枕木的安全负荷与它的厚度d的平方和宽度a的乘积成正比,与它的长度l的平方成反比. 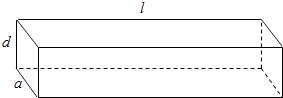
(1)在a>d>0的条件下,将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷会发生变化吗?变大还是变小?
(2)现有一根横截面为半圆(半圆的半径为R= ![]() )的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
)的柱形木材,用它截取成横截面为长方形的枕木,其长度即为枕木规定的长度l,问横截面如何截取,可使安全负荷最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=aex+ ![]() +b(a>0).
+b(a>0).
(1)求f(x)在[0,+∞)上的最小值;
(2)设曲线y=f(x)在点(2,f(2))的切线方程为3x﹣2y=0,求a、b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=sin2x+ ![]() sinxcosx+
sinxcosx+ ![]() ,x∈R,
,x∈R,
(1)求函数f(x)的最小正周期T及在[﹣π,π]上的单调递减区间;
(2)若关于x的方程f(x)+k=0,在区间[0, ![]() ]上且只有一个实数解,求实数k的取值范围.
]上且只有一个实数解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com