
【题目】已知关于x的不等式![]() 的解集中的整数解恰好有三个,则实数a的取值范围是______.
的解集中的整数解恰好有三个,则实数a的取值范围是______.
【答案】![]()
【解析】
由原不等式转化为[(4+2![]() )x-3][(4-2
)x-3][(4-2![]() )x-3]≤0,根据解集中的整数恰有3个,且为1,2,3,得到a的不等式,即可求解实数a的范围,得到答案.
)x-3]≤0,根据解集中的整数恰有3个,且为1,2,3,得到a的不等式,即可求解实数a的范围,得到答案.
由题知,![]() ,则(4x-3)2≤4ax2,即(4x-3)2-4ax2≤0,
,则(4x-3)2≤4ax2,即(4x-3)2-4ax2≤0,
即(4x-3+2![]() x)(4x-3-2
x)(4x-3-2![]() x)≤0,
x)≤0,
可得[(4+2![]() )x-3][(4-2
)x-3][(4-2![]() )x-3]≤0,
)x-3]≤0,
当a=2时,不等式为-24x+9≤0,解集为x![]() ,不是恰好有三个整数解.
,不是恰好有三个整数解.
当a≠2时,不等式为含x的一元二次不等式,此时
若![]() 时,即a=0时,不等式的解为x=
时,即a=0时,不等式的解为x=![]() 不是恰好有三个整数解.
不是恰好有三个整数解.
若0![]() 时,即0<a<4且a≠2时,不等式的解集为{x|
时,即0<a<4且a≠2时,不等式的解集为{x|![]() }
}
又∵![]() ,∴如果恰有三个整数解,只能是 1,2,3.
,∴如果恰有三个整数解,只能是 1,2,3.
∴![]() 解得:
解得:![]() .
.
若![]() 时,即a>4时,不等式的解集为{x|x
时,即a>4时,不等式的解集为{x|x![]() 或
或![]() }不会恰好有三个整数解.
}不会恰好有三个整数解.
综上所述,a的取值范围是[![]() ,
,![]() ).
).
故答案为:[![]() ,
,![]() ).
).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
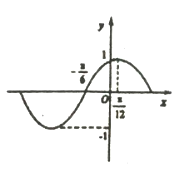
(1)求函数![]() 的解折式;
的解折式;
(2)在![]() 中,角
中,角![]() 满足
满足![]() ,且其外接圆的半径
,且其外接圆的半径![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴有两个不同的交点,其中一个交点坐标是
的图像与x轴有两个不同的交点,其中一个交点坐标是![]() ,且当
,且当![]() 时,恒有
时,恒有![]() .
.
(1)求不等式![]() 的解(用a、c表示);
的解(用a、c表示);
(2)若不等式![]() 对所有
对所有![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com