
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
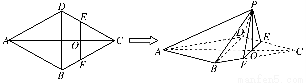
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
(1)见解析(2)4∶3
【解析】(1)证明:在菱形ABCD中,∵BD⊥AC,∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF,∴PO⊥平面ABFED,
∵BD?平面ABFED,∴PO⊥BD.
∵AO∩PO=O,所以BD⊥平面POA.
(2)连接OB,设AO∩BD=H.由(1)知,AC⊥BD.
∵∠DAB=60°,BC=4,∴BH=2,CH=2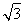 .
.
设OH=x(0<x<2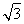 ).
).
由(1)知,PO⊥平面ABFED,∴PO⊥OB,即△POB为直角三角形.
∴PB2=OB2+PO2=(BH2+OH2)+PO2,
∴PB2=4+x2+(2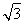 -x)2=2x2-4
-x)2=2x2-4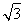 x+16=2(x-
x+16=2(x-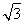 )2+10.
)2+10.
当x=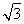 时,PB取得最小值,此时O为CH的中点.
时,PB取得最小值,此时O为CH的中点.
∴S△CEF=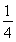 S△BCD,
S△BCD,
∴S梯形BFED=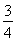 S△BCD=
S△BCD=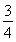 S△ABD,
S△ABD,
∴V1=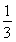 S△ABD·PO,V2=
S△ABD·PO,V2=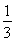 S梯形BFED·PO.
S梯形BFED·PO.
∴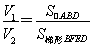 =
=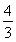 .
.
∴当PB取得最小值时,V1∶V2的值为4∶3.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
已知⊙P的半径等于6,圆心是抛物线y2=8x的焦点,经过点M(1,-2)的直线l将⊙P分成两段弧,当优弧与劣弧之差最大时,直线l的方程为( )
A.x+2y+3=0 B.x-2y-5=0
C.2x+y=0 D.2x-y-5=0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷6练习卷(解析版) 题型:选择题
由不等式组 围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
A.P′(t)>0 B.P′(t)<0 C.P′(t)=0 D.P′(t)符号不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:填空题
圆x2+y2-ax+2=0与直线l相切于点A(3,1),则直线l的方程为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:选择题
已知双曲线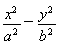 =1(a>0,b>0)的一个焦点与抛物线y2=4
=1(a>0,b>0)的一个焦点与抛物线y2=4 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.x2- =1 B.x2-y2=15 C.
=1 B.x2-y2=15 C. -y2=1 D.
-y2=1 D.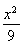 -
-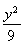 =1
=1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:解答题
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.
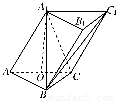
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=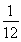 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷4练习卷(解析版) 题型:选择题
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )
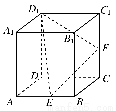
A.有无数条 B.有2条 C.有1条 D.不存在
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:填空题
在等差数列{an}中,已知a3+a8=10,则3a5+a7=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:填空题
已知集合A={x|x2-x≤0},函数f(x)=2-x(x∈A)的值域为B,则(∁RA)∩B=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com