
【题目】在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40![]() n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() (其中
(其中![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() n mile的位置C.
n mile的位置C.
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
【答案】(I)船的行驶速度为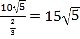 (海里/小时).(II)船会进入警戒水域.
(海里/小时).(II)船会进入警戒水域.
【解析】
试题(I)根据同角三角函数的基本关系式求出![]() ,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
(II)判断船是否会进入警戒水域,关键是看点E到直线l的距离与半径7的关系,因而可求出直线l的方程,以及E点坐标,然后再根据点到直线的距离公式得到结论.
(I)如图,AB=40![]() ,AC=10
,AC=10![]() ,
,![]()
由于![]() ,所以cos
,所以cos![]() =
=![]()
由余弦定理得BC=![]()
所以船的行驶速度为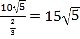 (海里/小时).
(海里/小时).
(II)解法一 如图所示,以A为原点建立平面直角坐标系,
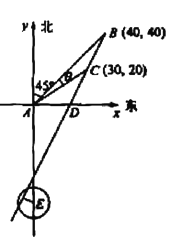
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1=![]() AB=40,
AB=40,
x2=ACcos![]() ,
,
y2=ACsin![]()
所以过点B、C的直线l的斜率k=![]() ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=![]()
所以船会进入警戒水域.
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,
![]() =
=![]() =
=![]() .
.
从而![]()
在![]() 中,由正弦定理得,AQ=
中,由正弦定理得,AQ=
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP![]() BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.![]()
在Rt![]() 中,PE=QE·sin
中,PE=QE·sin![]()
=![]() 所以船会进入警戒水域.
所以船会进入警戒水域.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() .点
.点![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,![]() .
.
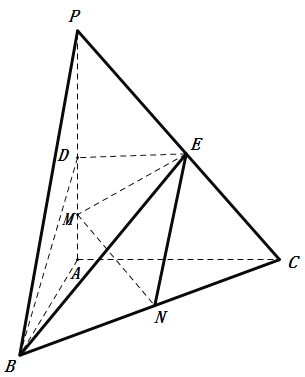
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列![]() 为函数
为函数![]() 图像上的点,点列
图像上的点,点列![]() 顺次为
顺次为![]() 轴上的点,其中
轴上的点,其中![]() ,对任意
,对任意![]() ,点
,点![]() 构成以
构成以![]() 为顶点的等腰三角形.
为顶点的等腰三角形.
(1)证明:数列![]() 是等比数列;
是等比数列;
(2)若数列![]() 中任意连续三项能构成三角形的三边,求
中任意连续三项能构成三角形的三边,求![]() 的取值范围;
的取值范围;
(3)求证:对任意![]() ,
,![]() 是常数,并求数列
是常数,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个半圆中有两个互切的内切半圆,由三个半圆弧围成曲边三角形,作两个内切半圆的公切线把曲边三角形分隔成两块,阿基米德发现被分隔的这两块的内切圆是同样大小的,由于其形状很像皮匠用来切割皮料的刀子,他称此为“皮匠刀定理”,如图,若![]() ,则阴影部分与最大半圆的面积比为( )
,则阴影部分与最大半圆的面积比为( )
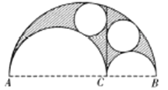
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 过椭圆
过椭圆![]() 的上,下顶点.
的上,下顶点.
(1)求椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于点的对称点为
关于点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
的斜率之和是否为定值,如果是,请求出此定值:如果不是,请说明理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的值域为
的值域为![]() .
.
(1)判断此函数的奇偶性,并说明理由;
(2)判断此函数![]() 在的单调性,并用单调性的定义证明你的结论;
在的单调性,并用单调性的定义证明你的结论;
(3)求出![]() 在
在![]() 上的最小值
上的最小值![]() ,并求
,并求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
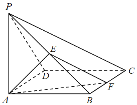
(1)求证:平面![]() 平面
平面![]() .
.
(2)试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com