
【题目】已知函数![]() 对任意
对任意![]() ,都有
,都有![]() .
.
(1)若函数![]() 的顶点坐标为
的顶点坐标为![]() 且
且![]() ,求
,求![]() 的解析式;
的解析式;
(2)函数![]() 的最小值记为
的最小值记为![]() ,求函数
,求函数![]() 在
在![]() 上的值域.
上的值域.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a、b∈R,a、b为常数),且y=f(x)在x=1处切线方程为y=x﹣1.
(a、b∈R,a、b为常数),且y=f(x)在x=1处切线方程为y=x﹣1.
(1)求a,b的值;
(2)设h(x)=![]() , k(x)=2h′(x)x2 , 求证:当x>0时,k(x)<
, k(x)=2h′(x)x2 , 求证:当x>0时,k(x)<![]() +
+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,
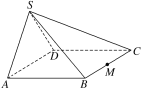
(1)求证:CD⊥平面SAD.
(2)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=![]() ,其中
,其中![]() ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,第一象限内有定点
中,第一象限内有定点![]() 和射线
和射线![]() ,已知
,已知![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 轴上的动点
轴上的动点![]() 与
与![]() ,
,![]() 共线.
共线.
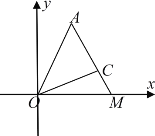
(1)求![]() 点坐标(用
点坐标(用![]() 表示);
表示);
(2)求![]() 面积
面积![]() 关于
关于![]() 的表达式
的表达式![]() ;
;
(3)求![]() 面积的最小时直线
面积的最小时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求A中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ=4cosθ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为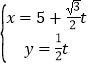 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P、Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1 , 焦点为F2;以F1 , F2为焦点,离心率e=![]() 的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
当m=1时,求椭圆C2的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
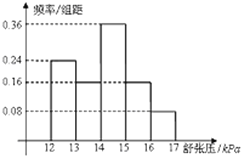
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com