练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线l1:ax－y＋2a=0与l2:(2a－1)x＋ay＋a=0互相垂直，求a的值.

    解法一:(1)当a≠0时，l1的斜率k1=a，l2的斜率k2=－.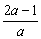

    ∵l1⊥l2，∴a·(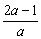－)=－1，a=1.

    (2)当a=0时，直线l1的斜率为0，l2的斜率不存在，两直线垂直.

    综上所述，a=0或a=1为所求.

    解法二:∵A1=a,B1=－1,A2=2a－1,B2=a,

    ∴由A1A2＋B1B2=0,得a(2a－1)－a=0,a=0或a=1.

    点评:利用k1·k2=－1判断两直线垂直时，两直线的斜率都必须存在.当两条直线中一条的斜率为0，另一条直线的斜率不存在时，两直线也垂直.本例利用A1A2＋B1B2=0求a的值更为快捷.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线l1:ax+2y+6=0与l2:x+(a-1)y+a2-1=0平行,则实数a的值是(    )

    A.-1或2                      B.0或1

    C.-1                           D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l1:ax-y-b=0,l2:bx-y+a=0,当a、b满足一定的条件时,它们的图形可以是图3-2-3中的(    )

                               图3-2-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l1:ax+3y+c=0与l2:2x-3y+4=0,若l1与l2的交点在y轴上,则c=________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0,

    （1）试判断l1与l2是否平行；

    （2）l1⊥l2时，求a的值.

    查看答案和解析>>

    同步练习册答案