
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() (
(![]() )过点
)过点![]() ,且椭圆
,且椭圆![]() 关于
关于
直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (异于椭圆
(异于椭圆![]() 的左、右顶点),线段
的左、右顶点),线段![]() 的中点为
的中点为![]() .点
.点![]() 是椭圆
是椭圆![]() 的右顶点.求直线
的右顶点.求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
①我离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室里取了作业本再回家;
②我放学回家骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;

③我放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
A.(1)(2)(4)B.(4)(1)(2)C.(4)(1)(3)D.(4)(2)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛,下面是他们的一段对话.甲说:“乙参加‘演讲’比赛”;乙说:“丙参加‘诗词’比赛”;丙说“丁参加‘演讲’比赛”;丁说:“戊参加‘诗词’比赛”;戊说:“丁参加‘诗词’比赛”.
已知这5个人中有2人参加“演讲”比赛,有3人参加“诗词”比赛,其中有2人说的不正确,且参加“演讲”的2人中只有1人说的不正确.根据以上信息,可以确定参加“演讲”比赛的学生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文中有回文句,如:“上海自来水来自海上”,倒过来读完全一样。数学中也有类似现象,如:88,454,7337,43534等,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”!
二位的回文数有11,22,33,44,55,66,77,88,99,共9个;
三位的回文数有101,111,121,131,…,969,979,989,999,共90个;
四位的回文数有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:11位的回文数总共有_________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校900名学生在一次百米测试中,成绩全部介于13秒与18 秒之间,利用分层抽样的方法抽取其中若干个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],有关数据见下表:
各组组员数 | 各组抽取人数 | |
[13,14) | 54 | a |
[14,15) | b | 8 |
[15,16) | 342 | 19 |
[16,17) | 288 | c |
[17,18] | d |
(1)求a,b,c,d的值;
(2)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
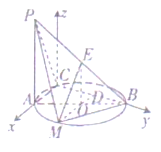
【题目】如图所示,![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在弧
在弧![]() 上,且
上,且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:
(1)由△ABC中位线的性质可得![]() ,则
,则![]() 平面
平面![]() .由线面平行的判断定理可得
.由线面平行的判断定理可得![]() 平面
平面![]() .结合面面平行的判断定理可得
.结合面面平行的判断定理可得![]() 平面
平面![]() .
.
(2)由圆的性质可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,据此可知
,据此可知![]() 平面
平面![]() .利用面面垂直的判断定理可得平面
.利用面面垂直的判断定理可得平面![]() 平面
平面![]() .
.
(3)以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .结合空间几何关系计算可得平面
.结合空间几何关系计算可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() .由图可知
.由图可知![]() 为锐角,故
为锐角,故![]() .
.
试题解析:
(1)证明:因为点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)证明:因为点![]() 在以
在以![]() 为直径的
为直径的![]() 上,所以
上,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)解:如图,以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
延长![]() 交
交![]() 于点
于点![]() .因为
.因为![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() .
.
因为 ,所以
,所以![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() .
.
同理可求平面![]() 的一个法向量
的一个法向量![]() .
.
所以![]() .由图可知
.由图可知![]() 为锐角,所以
为锐角,所以![]() .
.
【题型】解答题
【结束】
21
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
(1)求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;
垂直的直线方程;
(2)在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() 的左、右焦点分别为F1、F2,离心率为
的左、右焦点分别为F1、F2,离心率为![]() ,直线y=1与C的两个交点间的距离为
,直线y=1与C的两个交点间的距离为![]()
(1)求圆C的方程;
(2)如图,过F1、F2作两条平行线l1、l2与C的上半部分分别交于A、B两点,求四边形ABF2F1面积的最大值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com