练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给出条件：①；②；③；④；使得函数，对任意，都使成立的条件序号是（）

    A.①③B.②④C.③④D.②③

    【答案】B

    【解析】

    根据奇（偶）函数的定义判断出函数是偶函数，再判断出函数的单调性，利用偶函数图象关于y轴对称，判断所给的四个条件是否符合条件．

    ∵函数f（﹣x）＝sin2（﹣x）+（﹣x）2＝sin2x+x2＝f（x），

    ∴函数f（x）是偶函数

    又∵y＝sinx在上是增函数，y＝x2在上是增函数，

    ∴函数f（x）＝sin2x+x2在上是增函数，在上是减函数，

    故①x1＜x2，③x1＜|x2|中的条件都不能保证f（x1）＜f（x2）成立，

    对于②④，当，|x1|＜|x2|时，都有x12＜x22保证f（x1）＜f（x2）成立，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AD∥BC，ADC=PAB=90°，BC=CD=AD.E为棱AD的中点，异面直线PA与CD所成的角为90°.

    （I）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；

    (II)若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知多面体，，，均垂直于平面，，，，．

    （1）证明：⊥平面；

    （2）求直线与平面所成的角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为定义在实数集上的函数，把方程称为函数的特征方程，特征方程的两个实根、（），称为的特征根.

    （1）讨论函数的奇偶性，并说明理由；

    （2）已知为给定实数，求的表达式；

    （3）把函数，的最大值记作，最小值记作，研究函数，的单调性，令，若恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一列函数，设直线与的交点为，点在轴和直线上的射影分别为，记的面积为，的面积为.

    （1）求的最小值，并指出此时的取值；

    （2）在中任取一个函数，求该函数在上是增函数或在上是减函数的概率；

    （3）是否存在正整数，使得成立，若存在，求出的值，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

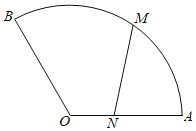
    【题目】某公园草坪上有一扇形小径（如图）,扇形半径为,中心角为,甲由扇形中心出发沿以每秒2米的速度向快走,同时乙从出发,沿扇形弧以每秒米的速度向慢跑,记秒时甲、乙两人所在位置分别为,，通过计算，判断下列说法是否正确：

    （1）当时，函数取最小值；

    （2）函数在区间上是增函数；

    （3）若最小，则；

    （4）在上至少有两个零点；

    其中正确的判断序号是______（把你认为正确的判断序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系，通过问卷调查，整理数据得如下列联表：

    （1）根据列联表，能否有99.9%的把握认为对手机游戏的兴趣程度与年龄有关?

    （2）若已经从40岁以下的被调查者中用分层抽样的方式抽取了5名，现从这5名被调查者中随机选取3名，求这3名被调查者中恰有1名对手机游戏无兴趣的概率.

    附：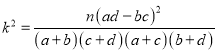

    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是（≈0.618，称为黄金分割比例)，著名的“断臂维纳斯”便是如此．此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是．若某人满足上述两个黄金分割比例，且腿长为105cm，头顶至脖子下端的长度为26 cm，则其身高可能是

    A. 165 cmB. 175 cmC. 185 cmD. 190cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)=ax2-a-lnx，其中a ∈R.

    （I）讨论f(x)的单调性；

    （II）确定a的所有可能取值，使得在区间（1，+∞）内恒成立(e=2.718…为自然对数的底数)。

    查看答案和解析>>

    同步练习册答案