
【题目】(导学号:05856301)已知函数f(x)=m(x-1)ex+![]() x2(m∈R),其导函数为f′(x),若对任意的x<0,不等式x2+(m+1)x>f′(x)恒成立,则实数m的取值范围为( )
x2(m∈R),其导函数为f′(x),若对任意的x<0,不等式x2+(m+1)x>f′(x)恒成立,则实数m的取值范围为( )
A. (0,1) B. (-∞,1) C. (-∞,1] D. (1,+∞)
【答案】C
【解析】由题意得f′(x)=mex+m(x-1)ex+x=mxex+x,
所以x2+(m+1)x>f′(x)对任意的x<0恒成立等价于mxex+x<x2+(m+1)x对任意的x<0恒成立,
即mex-x-m>0对任意的x<0恒成立.
令g(x)=mex-x-m(x<0),则g′(x)=mex-1,
当m≤1时,g′(x)=mex-1≤ex-1<0,则g(x)在(-∞,0)上单调递减,所以g(x)>g(0)=0,符合题意;
当m>1时,g(x)在(-∞,-ln m)上单调递减,在(-ln m,0)上单调递增,所以g(x)min=g(-ln m)<g(0)=0,不合题意.
所以实数m的取值范围为(-∞,1].
故选:C


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】下列命题中的假命题是( )
A. α,β∈R,使sin(α+β)=sinα+sinβ
B. φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
C. x0∈R,使![]() (a,b,c∈R且为常数)
(a,b,c∈R且为常数)
D. a>0,函数f(x)=ln2x+lnx-a有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,∠DAB=60°.
(1)求证:直线AM∥平面PNC;
(2)求二面角D﹣PC﹣N的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
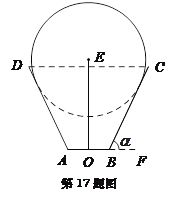
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
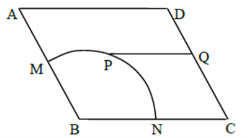
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区![]() ,其中
,其中![]() 是半径为1百米的扇形,
是半径为1百米的扇形,![]() . 管理部门欲在该地从
. 管理部门欲在该地从![]() 到
到![]() 修建小路:在弧
修建小路:在弧![]() 上选一点
上选一点![]() (异于
(异于![]() 两点),过点
两点),过点![]() 修建与
修建与![]() 平行的小路
平行的小路![]() .问:点
.问:点![]() 选择在何处时,才能使得修建的小路
选择在何处时,才能使得修建的小路![]() 与
与![]() 及
及![]() 的总长最小?并说明理由.
的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856310)
已知函数f(x)=x+![]() +ln x(a∈R).
+ln x(a∈R).
(Ⅰ)当a=2时, 求函数f(x)的单调区间;
(Ⅱ)若关于x的函数g(x)=![]() -f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
-f(x)+ln x+2e(e为自然对数的底数)有且只有一个零点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856323)已知在△ABC中,A,B,C所对的边分别为a,b,c,R为△ABC外接圆的半径,若a=1, ![]() sin2B+
sin2B+![]() sin2C-sin2A=sin Asin Bsin C,则R的值为( )
sin2C-sin2A=sin Asin Bsin C,则R的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
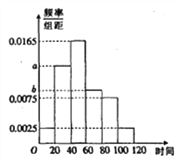
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com