
 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数. 时,求
时,求 的最大值和最小值;
的最大值和最小值; ,求实数k的取值范围.
,求实数k的取值范围.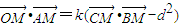 ,整理即可求出动点M的轨迹方程为(1-k)(x2-2x)+y2=0,再分情况得出曲线类型;
,整理即可求出动点M的轨迹方程为(1-k)(x2-2x)+y2=0,再分情况得出曲线类型;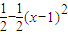 ,再把
,再把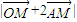 整理为
整理为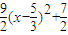 ,利用二次函数在闭区间上的最值求即可求出
,利用二次函数在闭区间上的最值求即可求出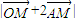 的最大值和最小值;
的最大值和最小值;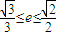 ,得圆锥曲线是椭圆,且方程可化为
,得圆锥曲线是椭圆,且方程可化为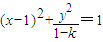 .再利用离心率e和系数的关系分情况分别求出对应的实数k的取值范围即可.
.再利用离心率e和系数的关系分情况分别求出对应的实数k的取值范围即可. ,
,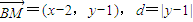 ,
,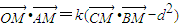
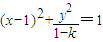 ,当k>1时,动点M的轨迹是双曲线;
,当k>1时,动点M的轨迹是双曲线;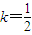 时,M的轨迹方程为
时,M的轨迹方程为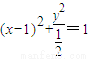 ,.得:0≤x≤2,y2=
,.得:0≤x≤2,y2= .
.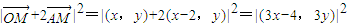
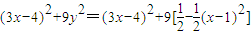
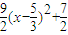 .
.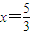 时,
时,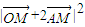 取最小值
取最小值
 取最大值16.
取最大值16.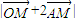 的最小值是
的最小值是 ,最大值是4.
,最大值是4.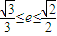 ,即e<1,此时圆锥曲线是椭圆,其方程可化为
,即e<1,此时圆锥曲线是椭圆,其方程可化为 ,
,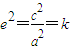 ,∵
,∵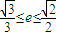 ,∴
,∴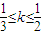 ;
;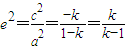 ,∵
,∵ ,∴
,∴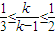 ,而k<0得,
,而k<0得,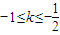 .
.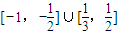 .
.

科目:高中数学 来源:湖南省炎德英才大联考2009届高三第八次月考数学试题(理) 题型:044
已知向量![]() ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足![]() ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.
(1)求动点M的轨迹方程;
(2)当![]() 时,若直线AC与动点M的轨迹相交于A、D两点,线段AD的垂直平分线交x轴E,求
时,若直线AC与动点M的轨迹相交于A、D两点,线段AD的垂直平分线交x轴E,求![]() 的取值范围;
的取值范围;
(3)如果动点M的轨迹是一条圆锥曲线,其离心率e满足![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
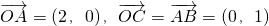 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足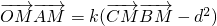 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数. 时,求
时,求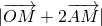 的最大值和最小值;
的最大值和最小值;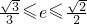 ,求实数k的取值范围.
,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源:2011年陕西省西安市西工大附中高考数学七模试卷(解析版) 题型:解答题
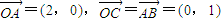 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数. 时,求
时,求 的最大值和最小值;
的最大值和最小值;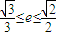 ,求实数k的取值范围.
,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源:辽宁省大连二十四中2009届高三第五次模拟考试(理) 题型:解答题
已知向量 ,动点M到定直线
,动点M到定直线 的距离等于
的距离等于 ,并且满足
,并且满足 ,其中
,其中 为坐标原点,
为坐标原点, 为非负实数.
为非负实数.
(I)求动点M的轨迹方程 ;
;
(II)若将曲线 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(III)若(II)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足 ,当
,当 是曲线
是曲线 的两个焦点时,则曲线
的两个焦点时,则曲线 上恒存在点P,使得
上恒存在点P,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com