
(本小题满分14分)给定函数
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足, 求证:
求证: ;
;
(3)设 ,
, 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。
(1)  的定义域为
的定义域为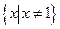 ………1分 (此处不写定义域,结果正确不扣分)
………1分 (此处不写定义域,结果正确不扣分) 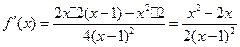 …………3分
…………3分
由 得
得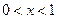 或
或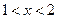
单调减区间为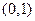 和
和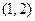 ………5分(答案写成(0,2)扣1分;不写区间形式扣1分)
………5分(答案写成(0,2)扣1分;不写区间形式扣1分)
(2)由已知可得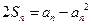 , 当
, 当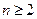 时,
时,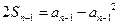
两式相减得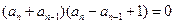
∴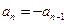 或
或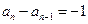
当 时,
时,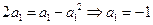 ,若
,若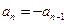 ,则
,则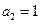 这与题设矛盾
这与题设矛盾
∴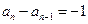 ∴
∴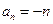 ……8分
……8分
于是,待证不等式即为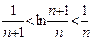 。
。
为此,我们考虑证明不等式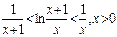
令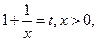 则
则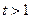 ,
,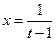
再令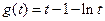 ,
,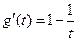 由
由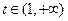 知
知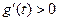
∴当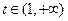 时,
时,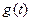 单调递增 ∴
单调递增 ∴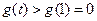 于是
于是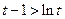
即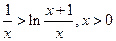 ①
①
令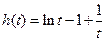 ,
,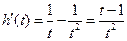 由
由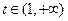 知
知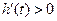
∴当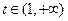 时,
时,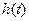 单调递增 ∴
单调递增 ∴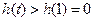
 于是
于是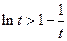
即 ②
②
由①、②可知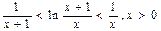 ………………10分
………………10分
所以,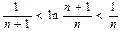 ,即
,即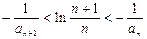 ………………11分
………………11分
(3)由(2)可知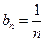 则
则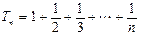 ……12分
……12分
在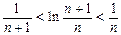 中令n=1,2,3…………..2010,2011并将各式相加得
中令n=1,2,3…………..2010,2011并将各式相加得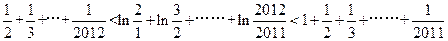 ……13分
……13分
即  ………………14分
………………14分
解析


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分) 设函数f (x)=ln x+ 在(0,
在(0,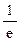 ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+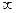 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-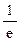 .
.
注:e是自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
已知函数 ,
, ,
,
(Ⅰ)当 时,若
时,若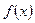 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当 是整数时,存在
是整数时,存在 ,使得
,使得 是
是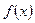 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在 ,且
,且 上的函数
上的函数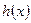 ,使当
,使当 时,
时,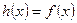 ,当
,当 时,
时,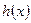 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数f(x)=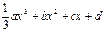 ,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,且a>0,d>0.设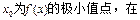 [1-
[1-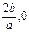 ]上,
]上,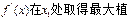 ,在
,在
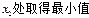 ,将点
,将点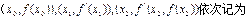 A, B, C,
A, B, C,
(Ⅰ)求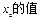
(II)若⊿ABC有一边平行于x轴,且面积为 ,求a ,d的值.
,求a ,d的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com