
【题目】已知函数![]() ,
,![]() .
.
(1)求证:![]() 在区间
在区间![]() 上无零点;
上无零点;
(2)求证:![]() 有且仅有2个零点.
有且仅有2个零点.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
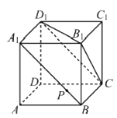
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上移动,有下列判断:①平面
上移动,有下列判断:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱锥
;③三棱锥![]() 的体积不变;④
的体积不变;④![]() 平面
平面![]() .其中,正确的是______.(把所有正确的判断的序号都填上)
.其中,正确的是______.(把所有正确的判断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市10月1日至14日的空气质量指数趋势图,空气质量指数越小表示空气质量越好,空气质量指数小于100表示空气质量优良,下列叙述中不正确的是( )
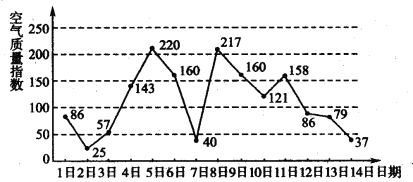
A.这14天中有7天空气质量优良
B.这14天中空气质量指数的中位数是103
C.从10月11日到10月14日,空气质量越来越好
D.连续三天中空气质量指数方差最大的是10月5日至10月7日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]()
![]() 的长轴
的长轴![]() ,长为4,过椭圆的右焦点
,长为4,过椭圆的右焦点![]() 作斜率为
作斜率为![]() (
(![]() )的直线交椭圆于
)的直线交椭圆于![]() 、
、![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
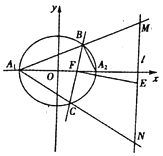
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 相交于
相交于![]() 、
、![]() 两点,设
两点,设![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com