
【题目】现有5名男生、2名女生站成一排照相,
(1)两女生要在两端,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)分两步,两端的两个位置,女生任意排,有![]() 种排法,中间的五个位置男生任意排,有
种排法,中间的五个位置男生任意排,有![]() 排法,利用分步计数乘法原理可得结果;(2)先将
排法,利用分步计数乘法原理可得结果;(2)先将![]() 名男生全排列,利用插空法,把
名男生全排列,利用插空法,把![]() 名女生插入到
名女生插入到![]() 名形成的
名形成的![]() 个空中的
个空中的![]() 个即可;(3) 采用去杂法,在七个人的全排列中,去掉女生甲在左端的
个即可;(3) 采用去杂法,在七个人的全排列中,去掉女生甲在左端的![]() 个,再去掉女生乙在右端的
个,再去掉女生乙在右端的![]() 个,但女生甲在左端同时女生乙在右端的
个,但女生甲在左端同时女生乙在右端的![]() 种排除了两次,要找回来一次.
种排除了两次,要找回来一次.
试题解析:(1)两端的两个位置,女生任意排,中间的五个位置男生任意排, ![]() (种).
(种).
(2)把男生任意全排列,然后在六个空中(包括两端)有顺序地插入两名女生;![]() (种).
(种).
(3)采用去杂法,在七个人的全排列中,去掉女生甲在左端的![]() 个,再去掉女生乙在右端的
个,再去掉女生乙在右端的![]() 个,但女生甲在左端同时女生乙在右端的
个,但女生甲在左端同时女生乙在右端的![]() 种排除了两次,要找回来一次.
种排除了两次,要找回来一次.
![]() (种).
(种).


科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ=4cosθ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为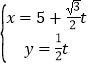 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P、Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(sinx+cosx)﹣![]() .
.
(1)若0<α<![]() , 且sinα=
, 且sinα=![]() , 求f(α)的值;
, 求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
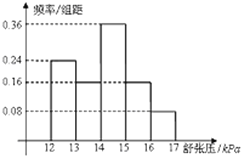
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学5次综合测评的成绩如茎叶图所示.
甲 | 乙 | |||||
9 | 8 | 8 | 3 | 3 | 7 | |
2 | 1 | 0 | 9 | ● | 9 |
老师在计算甲、乙两人平均分时,发现乙同学成绩的一个数字无法看清.若从{0,1,2,…,9}随机取一个数字代替,则乙的平均成绩超过甲的平均成绩的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c∈(0,+∞).
(1)若a=6,b=5,c=4是△ABC边BC,CA,AB的长,证明:cosA∈Q;
(2)若a,b,c分别是△ABC边BC,CA,AB的长,若a,b,c∈Q时,证明:cosA∈Q;
(3)若存在λ∈(-2,2)满足c2=a2+b2+λab,证明:a,b,c可以是一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+lnx.
(Ⅰ)当a=﹣1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-![]() 的下方,求a的取值范围;
的下方,求a的取值范围;
(Ⅲ)记f′(x)为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1 , x2 , x3…xk , 使得f′(x1)+f′(x2)+f′(x3)+…+f′(xk)≥2012成立?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙两个项目,对甲项目每投资10万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为![]() ;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
;已知乙项目的利润与产品价格的调整有关,在每次调整中,价格下降的概率都是p(0<p<1),设乙项目产品价格在一年内进行两次独立的调整.记乙项目产品价格在一年内的下降次数为X,对乙项目每投资10万元,X取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量X1、X2分别表示对甲、乙两项目各投资10万元一年后的利润.
(1)求X1,X2的概率分布和均值E(X1),E(X2);
(2)当E(X1)<E(X2)时,求p的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com