
【题目】已知函数![]() 有两个极值点
有两个极值点![]() 。
。
(1)求![]() 的取值范围;
的取值范围;
(2)求证:![]() 。
。
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:第一问利用题中的条件函数有两个极值点,相当于导数等于零有两个解,对函数求导,再求二阶导,对函数图像的走向加以分析,最后求得结果,第二问构造相应的函数,研究函数的图像,找出其对应的最值,最后求得结果.
详解:(1)![]() ,设
,设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
因为函数![]() 有两个极值点,所以函数
有两个极值点,所以函数![]() 有两个零点,
有两个零点,
所以![]() ,所以
,所以![]() ,此时
,此时![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
因为![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
综上可得![]() 的取值范围是
的取值范围是![]() 。
。
(2)由(1)知![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,
,
且![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 上的减函数,
上的减函数,
所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]()


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】在一个盒子中有3个球,蓝球、红球、绿球各1个,从中随机地取出一个球,观察其颜色后放回,然后再随机取出1个球.
(1)用适当的符号表示试验的可能结果,写出试验的样本空间;
(2)用集合表示“第一次取出的是红球"的事件;
(3)用集合表示“两次取出的球颜色相同”的事件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
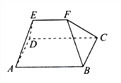
【题目】《九章算术》卷第五《商功》中有记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍,如图,四边形![]() 为正方形,四边形
为正方形,四边形![]() 、
、![]() 为两个全等的等腰梯形,
为两个全等的等腰梯形,![]() ,
,![]() ,若这个刍甍的体积为
,若这个刍甍的体积为![]() ,则
,则![]() 的长为( )
的长为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年底,共享单车日渐火爆起来,逐渐融入大家的日常生活中,某市针对18岁到80岁之间的不同年龄段的城市市民使用共享单车情况进行了抽样调查,结果如下表所示:

(1)采用分层抽样的方式从年龄在![]() 内的人中抽取
内的人中抽取![]() 人,求其中男性、女性的使用人数各为多少?
人,求其中男性、女性的使用人数各为多少?
(2)在(1)中选出![]() 人中随机抽取4人,求其中恰有2人是女性的概率;
人中随机抽取4人,求其中恰有2人是女性的概率;
(3)用样本估计总体,在全市18岁到80岁的市民中抽4人其中男性使用的人数记为![]() ,求
,求![]() 的分布列。
的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
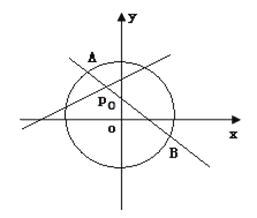
【题目】已知圆O:x2+y2=8内有一点P0(﹣1,2),AB为过点P0且倾斜角为α的弦.
(1)当α=135°时,求弦AB的长;
(2)当弦AB被P0平分时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行,来自151个国家和地区的3617家企业参展,规模和品质均超过首届.更多新产品、新技术、新服务“全球首发,中国首展”,专(业)精(品)尖(端)特(色)产品精华荟萃.某跨国公司带来了高端空调模型参展,通过展会调研,中国甲企业计划在2020年与该跨国公司合资生产此款空调.生产此款空调预计全年需投入固定成本260万元,每生产x千台空调,需另投入资金![]() 万元,且
万元,且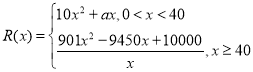 .经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
.经测算生产10千台空调需另投入的资金为4000万元.由调研知,每台空调售价为0.9万元时,当年内生产的空调当年能全部销售完.
(1)求2020年的企业年利润![]() (万元)关于年产量x(千台)的函数关系式;
(万元)关于年产量x(千台)的函数关系式;
(2)2020年产量为多少(千台)时,企业所获年利润最大?最大年利润是多少?注:利润=销售额–成本
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com