
【题目】已知函数f(x)=1+x﹣ ![]() +…+
+…+ ![]() ,g(x)=1﹣x+
,g(x)=1﹣x+ ![]() ﹣…﹣
﹣…﹣ ![]() ,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
,设函数F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.9
B.10
C.11
D.12
【答案】D
【解析】解∵f(0)=1>0,f(﹣1)=1﹣1﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() <0,
<0,
∴函数f(x)在区间(﹣1,0)内有零点;
当x∈(﹣1,0)时,f′(x)= ![]() >0,
>0,
∴函数f(x)在区间(﹣1,0)上单调递增,
故函数f(x)有唯一零点x∈(﹣1,0);
∵g(1)=1﹣1+ ![]() ﹣
﹣ ![]() +…﹣
+…﹣ ![]() >0,
>0,
g(2)=1﹣2+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() <0.
<0.
当x∈(1,2)时,f′(x)=﹣1+x﹣x2+x3﹣…+x2016﹣x2017= ![]() >0,
>0,
∴函数g(x)在区间(1,2)上单调递增,故函数g(x)有唯一零点x∈(1,2);
∵F(x)=f(x+4)g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,
∴f(x+4)的零点在(﹣5,﹣4)内,g(x﹣5)的零点在(6,7)内,
因此F(x)=f(x+4)g(x﹣5)的零点均在区间[﹣5,7]内,
∴b﹣a的最小值为7﹣(﹣5)=12.
故选:D.


科目:高中数学 来源: 题型:
【题目】如图所示,抛物线![]() 的焦点为
的焦点为![]() .
.
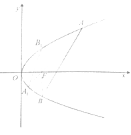
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的两条直线分别与抛物线
的两条直线分别与抛物线![]() 交于点
交于点![]() ,
,![]() 与
与![]() ,
,![]() (点
(点![]() ,
,![]() 在
在![]() 轴的上方).
轴的上方).
①若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
②设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点B(0,1).
,且过点B(0,1).

(Ⅰ)求椭圆的方程;
(Ⅱ)若点A是椭圆的右顶点,点![]() 在以AB为直径的圆上,延长PB交椭圆E于点Q,求
在以AB为直径的圆上,延长PB交椭圆E于点Q,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比三角形中的性质:(1)两边之和大于第三边;(2)中位线长等于底边的一半;(3)三内角平分线交于一点; 可得四面体的对应性质:(1)任意三个面的面积之和大于第四个面的面积;(2)过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的![]() ;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
;(3)四面体的六个二面角的平分面交于一点。其中类比推理结论正确的有 ( )
A. (1) B. (1)(2) C. (1)(2)(3) D. 都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程 ![]() =1表示的曲线为C,给出以下四个判断:
=1表示的曲线为C,给出以下四个判断:
①当1<t<4时,曲线C表示椭圆;
②当t>4或t<1时曲线C表示双曲线;
③若曲线C表示焦点在x轴上的椭圆,则1<t< ![]() ;
;
④若曲线C表示焦点在x轴上的双曲线,则t>4,
其中判断正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点B与点A(﹣1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知h(x)=|2x﹣1|+m|x+3|(m>0),且h(x)的最小值是7. (Ⅰ)求m的值;
(Ⅱ)求出当h(x)取得最小值时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com