
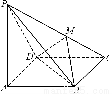
如图所示,在四棱锥PABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:填空题
已知实数x、y满足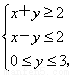 则z=2x+y的最小值是________.
则z=2x+y的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:填空题
已知空间四边形OABC,点M、N分别是OA、BC的中点,且 =a,
=a,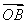 =b,
=b, =c,用a,b,c表示向量
=c,用a,b,c表示向量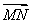 =________.
=________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
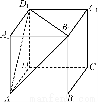
如图所示,正方体ABCDA1B1C1D1的棱长为6,则以正方体ABCDA1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,在正三棱柱ABCDEF中,AB=2,AD=1.P是CF的延长线上一点,FP=t.过A、B、P三点的平面交FD于M,交FE于N.
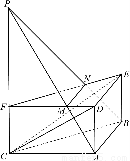
(1)求证:MN∥平面CDE;
(2)当平面PAB⊥平面CDE时,求t的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
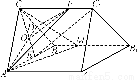
(1)求证:C1E∥平面ADF;
(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:填空题
设a、b为不重合的两条直线,α、β为不重合的两个平面,给出下列命题:
①若a∥α且b∥α,则a∥b;②若a⊥α且b⊥α,则a∥b;③若a∥α且a∥β,则α∥β;④若a⊥α且a⊥β,则α∥β.其中为真命题的是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:填空题
P为△ABC所在平面外一点,O为P在平面ABC内的射影.
(1)若P到△ABC三边距离相等,且O在△ABC的内部,则O是△ABC的________心;
(2)若PA⊥BC,PB⊥AC,则O是△ABC的________心;
(3)若PA,PB,PC与底面所成的角相等,则O是△ABC的________心.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:解答题
已知数列{an}满足a1+a2+…+an=n2(n∈N*).
(1)求数列{an}的通项公式;
(2)对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使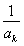 ,
,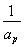 ,
,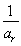 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com