
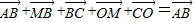
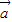 =(6,2)与
=(6,2)与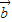 =(-3,k)的夹角是钝角,则k的取值范围是k<0
=(-3,k)的夹角是钝角,则k的取值范围是k<0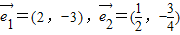 能作为平面内所有向量的一组基底
能作为平面内所有向量的一组基底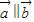 ,则
,则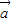 在
在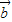 上的投影为
上的投影为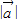 .
. 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
| A、在循环结构中,直到型先判断条件,再执行循环体,当型先执行循环体,后判断条件 | ||
| B、做n次随机试验,事件A发生m次,则事件A发生的频率m/n就是事件A发生的概率 | ||
C、从含有2008个个体的总体中抽取一个容量为100的本,现采用系统抽样方法应先剔除8人,则每个个体被抽到的概率均为
| ||
| D、如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数改变,方差不变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com