
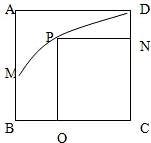
 如图,四边形ABCD是一块边长为4的正方形地域,地域内有一条河流MD,其经过的路线是以AB中点M为顶点,且开口向右的抛物线(河流宽度不计).某公司准备建一大型游乐园PQCN,问如何施工,才能使游乐园面积最大?并求出最大的面积.
如图,四边形ABCD是一块边长为4的正方形地域,地域内有一条河流MD,其经过的路线是以AB中点M为顶点,且开口向右的抛物线(河流宽度不计).某公司准备建一大型游乐园PQCN,问如何施工,才能使游乐园面积最大?并求出最大的面积. 科目:高中数学 来源: 题型:
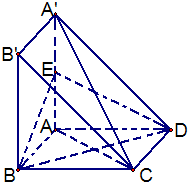 如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.
如图,四边形ABCD与A′ABB′都是边长为a的正方形,点E是A′A的中点,A′A⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
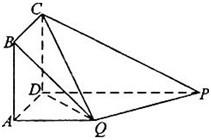 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
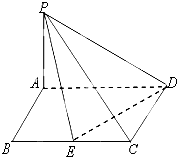 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
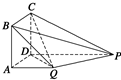 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com