
【题目】某公司一年经销某种商品,年销售量400吨,每吨进价5万元,每吨销售价8万元.全年进货若干次,每次都购买x吨,运费为每次2万元,一年的总存储费用为2x万元.
(1)求该公司经销这种商品一年的总利润y与x的函数关系;
(2)要使一年的总利润最大,则每次购买量为多少?并求出最大利润.
【答案】
(1)解:某公司一年购买某种货物400吨,每次都购买x吨,则需要购买 ![]() 次,运费为2万元/次,一年的总存储费用为2x万元,一年的总运费与总存储费用之和为
次,运费为2万元/次,一年的总存储费用为2x万元,一年的总运费与总存储费用之和为 ![]() 2+2x万元.
2+2x万元.
∴该公司经销这种商品一年的总利润y与x的函数关系y=1200﹣( ![]() 2+2x)
2+2x)
(2)解:要使一年的总利润最大,只要一年的总运费与总存储费用之和最小.
∵ ![]() 2+2x≥80,当
2+2x≥80,当 ![]() 2=2x即x=20吨时,等号成立.
2=2x即x=20吨时,等号成立.
∴每次购买20吨时,一年的总运费与总存储费用之和最小,最大利润1120万元
【解析】(1)先设某公司每次都购买x吨,由于一年购买某种货物400吨,得出需要购买的次数,从而求得一年的总运费与总存储费用之和,即可求出该公司经销这种商品一年的总利润y与x的函数关系;(2)利用基本不等式求得一年的总运费与总存储费用之和最小即可.


科目:高中数学 来源: 题型:
【题目】正三棱锥P﹣ABC中,CM=2PM,CN=2NB,对于以下结论:
①二面角B﹣PA﹣C大小的取值范围是(![]() , π);
, π);
②若MN⊥AM,则PC与平面PAB所成角的大小为![]() ;
;
③过点M与异面直线PA和BC都成![]() 的直线有3条;
的直线有3条;
④若二面角B﹣PA﹣C大小为![]() , 则过点N与平面PAC和平面PAB都成
, 则过点N与平面PAC和平面PAB都成![]() 的直线有3条.
的直线有3条.
正确的序号是 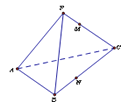
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x,y)是区域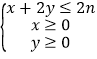 , (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
, (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
证明:数列{an﹣2}为等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习兴趣小组开展“学生语文成绩与外语成绩的关系”的课题研究,考察该校高二年级800名学生上学期期末的语文和外语成绩,按是否优秀分类得结果:语文和外语成绩都优秀的有60人,语文成绩优秀但外语成绩不优秀的有140人,外语成绩优秀但语文成绩不优秀的有100人.
(Ⅰ)能否有![]() 的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记所抽取的成绩中,语文、外语两科成绩至少有一科优秀的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
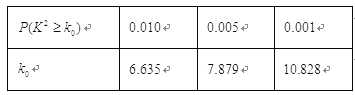
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的各项均为正数,且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,S2=
,S2= ![]() ,S3=
,S3= ![]() .设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
.设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
(1)试求数列{an}的通项;
(2)求T=[log21]+[log22]+[log23]+…+[log2( ![]() ﹣1)]+[log2(
﹣1)]+[log2( ![]() )]关于n的表达式.
)]关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A=[0,![]() ),B=[
),B=[![]() , 1],函数f (x)=
, 1],函数f (x)=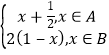 , 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
, 若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
A.(0,![]() ]
]
B.[![]() ,
, ![]() ]
]
C.(![]() ,
, ![]() )
)
D.[0,![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com