
【题目】某班有50名学生,男女人数不相等。随机询问了该班5名男生和5名女生的某次数学测试成绩,用茎叶图记录如下图所示,则下列说法一定正确的是( )

A. 这5名男生成绩的标准差大于这5名女生成绩的标准差。
B. 这5名男生成绩的中位数大于这5名女生成绩的中位数。
C. 该班男生成绩的平均数大于该班女生成绩的平均数。
D. 这种抽样方法是一种分层抽样。
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 中
中![]() ,
,![]() 为
为![]() 的中点.
的中点.
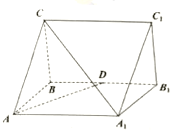
(1)求证:![]() ;
;
(2)若点![]() 为四边形
为四边形![]() 内部及其边界上的点,且三棱锥
内部及其边界上的点,且三棱锥![]() 的体积为三棱柱
的体积为三棱柱![]() 体积的
体积的![]() ,试在图中画出
,试在图中画出![]() 点的轨迹,并说明理由.
点的轨迹,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,求满足如下条件的最小四位整数![]() :第2017行的第
:第2017行的第![]() 项为2的正整数幂.已知
项为2的正整数幂.已知![]() ,那么该款软件的激活码是( )
,那么该款软件的激活码是( )

A. 1040 B. 1045 C. 1060 D. 1065
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 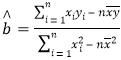 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
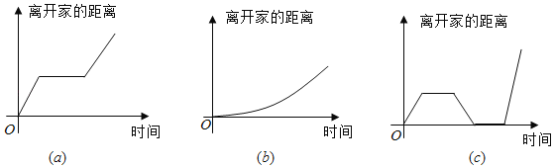
【题目】下述三个事件按顺序分别对应三个图象,正确的顺序是( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,左顶点B与右焦点
,左顶点B与右焦点![]() 之间的距离为3.
之间的距离为3.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 交
交![]() 轴于点
轴于点![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于两点
相交于两点![]() ,连接
,连接![]() 并延长分别与直线
并延长分别与直线![]() 交于两点
交于两点![]() . 若
. 若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 成等差数列(
成等差数列(![]() 、
、![]() 为正整数且
为正整数且![]() ),求
),求![]() 和
和![]() 的值;
的值;
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在实数
项和,是否存在实数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com