
【题目】如图:椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,它们在
,它们在![]() 轴右侧有两个交点
轴右侧有两个交点![]() 、
、![]() ,满足
,满足![]() .将直线
.将直线![]() 左侧的椭圆部分(含
左侧的椭圆部分(含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() ,直线
,直线![]() 右侧的双曲线部分(不含
右侧的双曲线部分(不含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() .以
.以![]() 为端点作一条射线,分别交
为端点作一条射线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (点
(点![]() 在第一象限),设此时
在第一象限),设此时![]() .
.
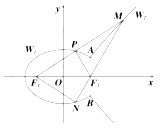
(1)求![]() 的方程;
的方程;
(2)证明: ![]() ,并探索直线
,并探索直线![]() 与
与![]() 斜率之间的关系;
斜率之间的关系;
(3)设直线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【答案】(1)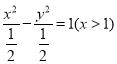 (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)根据椭圆方程求出右焦点![]() ,根据
,根据![]() 得到
得到![]() 、
、![]() 关于
关于![]() 轴对称,所以求出
轴对称,所以求出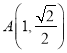 ,
, 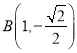 ,所以求出双曲线的方程;(2)设
,所以求出双曲线的方程;(2)设![]()
![]() ,得
,得![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,又因为
,又因为![]()
![]() 分别在曲线
分别在曲线![]() 和
和![]() 上,有,
上,有,
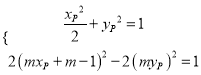 ,消去
,消去![]() ,得,
,得, ![]() (*),所以
(*),所以![]() 点坐标为
点坐标为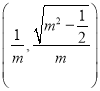 ,
, 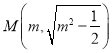 .所以直线
.所以直线![]() 的斜率
的斜率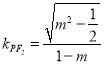 ,直线
,直线![]() 的斜率
的斜率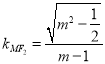 .所以
.所以![]() 与
与![]() 斜率之和为零;(3)由(2)知直线
斜率之和为零;(3)由(2)知直线![]() 与
与![]() 关于
关于![]() 轴对称,结合椭圆的对称性知点
轴对称,结合椭圆的对称性知点![]() 与点
与点![]() 关于
关于![]() 轴对称,故
轴对称,故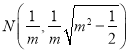 ,所以
,所以![]()
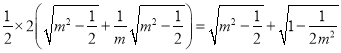 ,利用函数单调求出
,利用函数单调求出![]() 的范围。
的范围。
试题解析:(1)由条件,得![]() ,根据
,根据![]() 知,
知, ![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
且由椭圆与双曲线的对称性知, ![]() 、
、![]() 关于
关于![]() 轴对称,
轴对称,
故![]() 所在直线为
所在直线为![]() ,从而得
,从而得 ,
, 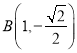 .
.
所以, ![]() ,又因为
,又因为![]() 为双曲线的焦点,所以
为双曲线的焦点,所以![]() ,
,
解得![]() .
.
因此, ![]() 的方程为
的方程为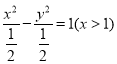 .
.
(2)由![]()
![]() ,得
,得![]() ,
, ![]() ,
,
由条件,得![]() ,即
,即![]() ,
,
由![]()
![]() 分别在曲线
分别在曲线![]() 和
和![]() 上,有,
上,有,
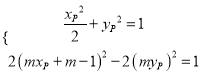 ,消去
,消去![]() ,得,
,得,
![]() (*),
(*),
将![]() 代入方程(*),成立,因此(*)有一根
代入方程(*),成立,因此(*)有一根![]() ,结合韦达定理得另一根为
,结合韦达定理得另一根为![]() ,因为
,因为![]() ,所以
,所以![]() ,舍去.
,舍去.
所以, ![]() .
.
从而![]() 点坐标为
点坐标为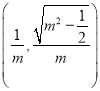 .
.
所以,直线![]() 的斜率
的斜率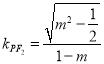 ,
,
由![]() ,得
,得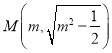 .
.
所以,直线![]() 的斜率
的斜率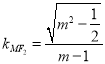 .
.
因此, ![]() 与
与![]() 斜率之和为零.
斜率之和为零.
(3)由(2)知直线![]() 与
与![]() 关于
关于![]() 轴对称,结合椭圆的对称性知点
轴对称,结合椭圆的对称性知点![]() 与点
与点![]() 关于
关于![]() 轴对称,故
轴对称,故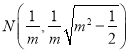 ,
,
因此, ![]()
 ,
,
![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() (cosx﹣sinx)sin(x+
(cosx﹣sinx)sin(x+![]() )﹣2asinx+b(a>0).
)﹣2asinx+b(a>0).
(1)若b=1,且对任意![]() , 恒有f(x)>0,求a的取值范围;
, 恒有f(x)>0,求a的取值范围;
(2)若f(x)的最大值为1,最小值为﹣4,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.
,如图2所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)已知函数![]() (
(![]() 为常数,
为常数,![]() )
)
(1)若![]() 是函数
是函数![]() 的一个极值点,求
的一个极值点,求![]() 的值;
的值;
(2)求证:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(3)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求正实数
成立,求正实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有正整数构成的数表如下:
第一行:1
第二行:1 2
第三行:1 1 2 3
第四行:1 1 2 1 1 2 3 4
第五行:1 1 2 1 1 2 3 1 1 2 1 1 2 3 4 5
…… …… ……
第![]() 行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,...,直至按原序抄写第
行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,...,直至按原序抄写第![]() 行,最后添上数
行,最后添上数![]() .(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).
.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).
将按照上述方式写下的第![]() 个数记作
个数记作![]() (如
(如![]() )
)
(1)用![]() 表示数表第
表示数表第![]() 行的数的个数,求数列
行的数的个数,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)第8行中的数是否超过73个?若是,用![]() 表示第8行中的第73个数,试求
表示第8行中的第73个数,试求![]() 和
和![]() 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(3)令![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
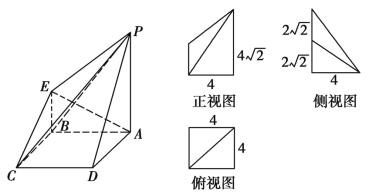
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com