
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,已知但
,已知但![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作斜率为的直线
作斜率为的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)由题得![]() ,
,![]() ,结合
,结合![]() ,解得
,解得![]() ,可得椭圆的方程.
,可得椭圆的方程.
(2)联立方程组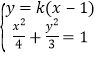 ,整理得
,整理得![]() ,设
,设![]() ,则
,则![]() ,把
,把![]() 坐标化,可得
坐标化,可得![]() ,代入整理得
,代入整理得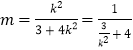 ,解得
,解得![]() ,可得解.
,可得解.
试题解析:(1)将![]() 代入
代入![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,结合
,结合![]() ,解得
,解得![]() ,
,
故椭圆的方程为![]() .
.
(2)设![]() ,联立方程组
,联立方程组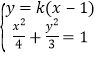 ,整理得
,整理得![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
由于菱形的对角线垂直,故![]() ,
,
故![]() ,即
,即![]() ,
,
即![]() ,
,
由已知条件知![]() 且
且![]() ,
,
所以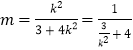 ,所以
,所以![]() ,
,
故存在满足题意的点![]() ,且
,且![]() 的取值范围是
的取值范围是![]() ,
,
当直线![]() 的斜率不存在时,不合题意.
的斜率不存在时,不合题意.
点睛:本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y=
,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y= ![]() 的定义域为
的定义域为 ![]() ;
;
②设A={0,1,2},B={x|f3(x)=x,x∈A},则A=B;
③ ![]() ;
;
④若集合M={x|f12(x)=x,x∈[0,2]},
则M中至少含有8个元素.( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是___________
![]() 用一个平面截一个球,得到的截面是一个圆;
用一个平面截一个球,得到的截面是一个圆;
![]() 圆台的任意两条母线延长后一定交于一点;
圆台的任意两条母线延长后一定交于一点;
![]() 有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
![]() 若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
![]() 用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
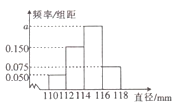
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+21nx.
(1)求f(x)的单调区间.
(2)若f(x)在(0,1]上的最大值是﹣2,求a的值.
(3)记g(x)=f(x)+(a﹣1)lnx+1,当a≤﹣2时,若对任意x1 , x2∈(0,+∞),总有|g(x1)﹣g(x2)|≥k|x1﹣x2|成立,试求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如图,试估计成绩高于11级分的人数为 ( )

A. 8 000 B. 10 000 C. 20 000 D. 60 000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com