
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 . 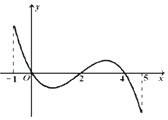
【答案】①②④
【解析】①②④解:对于①,∵由导函数的图象知,函数f(x)的最大值点为0与4,故①正确;
对于②,由已知中y=f′(x)的图象可得在[0,2]上f′(x)<0,即f(x)在[0,2]是减函数,即②正确;
对于③,由导函数y=f′(x)的图象可知,函数在[﹣1,0],[2,4]上为增函数,
则[0,2],[4,5]上为减函数,且函数在x=0和x=4取得极大值f(0)=2,f(4)=2,
在x=2取得极小值f(2)=0,则函数f(x)的大致图象如图:则函数y=f(x)与直线y=a的图象有四个交点可能为0、1、2、4个,即③错误
对于④,由已知中y=f′(x)的图象,及表中数据可得当x=0或x=4时,函数取最大值2,若x∈[﹣1,t]时,f(x)的最大值是2,那么0≤t≤5,故t的最大值为5,即④正确;
对于⑤,根据函数f(x)的大致图象,判断⑤错误;
所以答案是:①②④.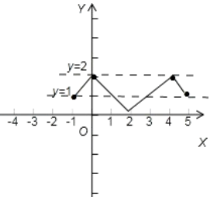
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
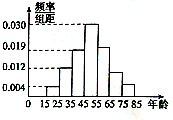
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=x0与g(x)=1
B.f(x)=x与g(x)= ![]()
C.f(x)=x2﹣1与g(x)=x2+1
D.f(x)=|x|与g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( ) 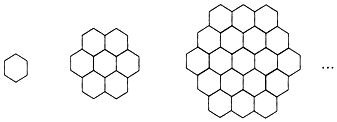
A.37 3n2﹣3n+1
B.38 3n2﹣3n+2
C.36 3n2﹣3n
D.35 3n2﹣3n﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个集合U,A,B及元素间的关系如图所示,则(CUA)∩B=( ) 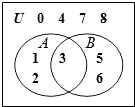
A.{5,6}
B.{3,5,6}
C.{3}
D.{0,4,5,6,7,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=sin (2x﹣ ![]() )(x∈R),给出下列三个结论: ①对于任意的x∈R,都有f(x)=cos (2x﹣
)(x∈R),给出下列三个结论: ①对于任意的x∈R,都有f(x)=cos (2x﹣ ![]() );
);
②对于任意的x∈in R,都有f(x+ ![]() )=f(x﹣
)=f(x﹣ ![]() );
);
③对于任意的x∈R,都有f( ![]() ﹣x)=f(
﹣x)=f( ![]() +x).
+x).
其中,全部正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x+y)=f(x)+f(y)且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
A.f(1)+2f(1)+…+nf(1)
B.f( ![]() )
)
C.n(n+1)
D.n(n+1)f(1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com