
����Ŀ��ijѧУΪ�˽�ѧУʳ�õķ�����������������50���Ͳ͵Ľ�ʦ��ѧ����������50��ʦ���Բ������������������֣����Ƴ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ���Ϊ[40��50����[50��60��������[90��100]�� 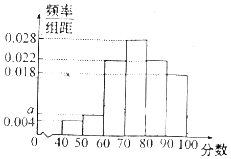
��1����Ƶ�ʷֲ�ֱ��ͼ��a��ֵ��
��2����������[40��60����ʦ���У������ȡ2�ˣ��������ǡ����1��������[40��50���ϵĸ��ʣ�
��3��ѧУ�涨��ʦ����ʳ�÷������������ֲ��õ���75�֣��������ڲ����٣������������ݹ��Ƹ�Уʦ����ʳ�÷����������ֵ�ƽ���֣����ݴ˻ش�ʳ���Ƿ���Ҫ�����ڲ����٣�
���𰸡�
��1���⣺�ɣ�0.004+a+0.022+0.028+0.022+0.018����10=1��
���a=0.006��
��2���⣺�豻��ȡ��2����ǡ����һ��������[40��50����Ϊ�¼�A����
��Ϊ������������[40��50����ʦ������Ϊ��m1=0.004��10��50=2����Ϊ1��2��
������������[50��60����ʦ������Ϊ��m2=0.006��10��50=3����Ϊ3��4��5�š�
���Դ�5��������ȡ2�˹��У�
��1��2������1��3������1��4������1��5������2��3������2��4����
��2��5������3��4������3��5������4��5����10�ֵȿ��������
2����ǡ��1��������[40��50�����У�
��1��3������1��4������1��5������2��3������2��4������2��5����6�ֵȿ��������
��2����ǡ����1��������[40��50���ϵĸ���ΪP��A��= ![]() =
= ![]() ��
��
��3���⣺�����������ֵ�ƽ����Ϊ��
![]() =45��0.004��10+55��0.006��10+65��0.022��10+75��0.028��10+85��0.022��10+95��0.018��10=76.2��
=45��0.004��10+55��0.006��10+65��0.022��10+75��0.028��10+85��0.022��10+95��0.018��10=76.2��
��76.2��75����ʳ�ò���Ҫ�ڲ����٣�
����������1����Ƶ�ʷֲ�ֱ��ͼ��С�������֮��Ϊ1�������a��ֵ����2���豻��ȡ��2����ǡ����һ��������[40��50����Ϊ�¼�A��������������[40��50����ʦ������Ϊ2����Ϊ1��2��������������[50��60����ʦ������Ϊ3����Ϊ3��4��5�ţ��ɴ������оٷ��������5��������ȡ2�ˣ�2����ǡ����1��������[40��50���ϵĸ��ʣ���3����������������ֵ�ƽ����Ϊ76.2��75���Ӷ��õ�ʳ�ò���Ҫ�ڲ����٣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OB��������·�����ƿ�������ֱ�ߣ��� ![]() ���ڡ�AOB����һ������P����С���Բ��ƣ�����֪P��ֱ��OA��OB�ľ���ֱ�ΪPD��PE��PD=6ǧ�ף�PE=12ǧ�ף��־���������P��һ��ֱ����С·����������·OA��OB�ֱ��ڵ�M��N��
���ڡ�AOB����һ������P����С���Բ��ƣ�����֪P��ֱ��OA��OB�ľ���ֱ�ΪPD��PE��PD=6ǧ�ף�PE=12ǧ�ף��־���������P��һ��ֱ����С·����������·OA��OB�ֱ��ڵ�M��N�� 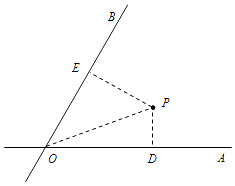
��1���������P��������·����O���ľ��룻
��2����������PΪС·MN���е㣬��С·MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() �ڣ���1��+�ޣ�����������
�ڣ���1��+�ޣ�����������
��1����b=1ʱ����a��ȡֵ��Χ��
��2����g��x��=f��x����1008û����㣬f��1��=0����f����3����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Բ������Ϊԭ��O��������x���ϣ��϶���ΪA�����ҽ���ֱ�ΪF1 �� F2 �� �߶�OF1 �� OF2���е�ֱ�ΪB1 �� B2 �� �ҡ�AB1B2�����Ϊ4��ֱ�������Σ���B1��l����Բ��P��Q���㣬ʹPB2��ֱQB2 �� ��ֱ��l�ķ��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a��b��c�ɵȱ����У��� ![]() ��ȡֵ��ΧΪ ��
��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�Sn����ǰn��ͣ���֪a1+a3=16��S4=28��
��1��������{an}��ͨ�ʽ
��2����nȡ��ֵʱSn������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�AA1�͵���ABC��AC��BC��AC=BC= ![]() AA1=2��D��AC���е㣮
AA1=2��D��AC���е㣮 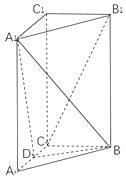
��1����֤��B1C��ƽ��A1BD��
��2����ֱ��AC��ƽ��A1BD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲�����A��B����ľ��룬�غӰ�ѡȡC��D���㣬���CD=2km����CDB=��ADB=30�㣬��ACD=60�㣬��ACB=45�㣬��A��B����ľ��룮 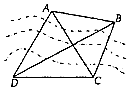
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բx2+y2=5x�ڣ����� ![]() ��n���ҵij��ȳɵȲ����У�����ҳ�Ϊ���е�����a1 �� ��ҳ�Ϊan �� ������
��n���ҵij��ȳɵȲ����У�����ҳ�Ϊ���е�����a1 �� ��ҳ�Ϊan �� ������ ![]() ����ôn��ȡֵ���� ��
����ôn��ȡֵ���� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com