
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,PA=2,∠ABC=90°,![]() ,BC=1,
,BC=1, ![]() ,∠ACD=60°,E为CD的中点.
,∠ACD=60°,E为CD的中点.

(1)求证:BC∥平面PAE;
(2)求点A到平面PCD的距离.
【答案】(1)见解析;(2)![]()
【解析】(1)证明:∵AB=![]() ,BC=1,∠ABC=90°,
,BC=1,∠ABC=90°,
∴AC=2,∠BCA=60°.
在△ACD中,∵AD=2![]() ,AC=2,∠ACD=60°,
,AC=2,∠ACD=60°,
∴AD2=AC2+CD2-2AC·CD·cos∠ACD,
∴CD=4,∴AC2+AD2=CD2,∴△ACD是直角三角形,
又E为CD中点,∴AE=![]() CD=CE,
CD=CE,
∵∠ACD=60°,∴△ACE为等边三角形,
∴∠CAE=60°=∠BCA,∴BC∥AE,
又AE平面PAE,BC平面PAE,∴BC∥平面PAE.
(2)设点A到平面PCD的距离为d,根据题意可得,
PC=2![]() ,PD=CD=4,∴S△PCD=2
,PD=CD=4,∴S△PCD=2![]() ,
,
∵VP-ACD=VA-PCD,∴![]() ·S△ACD·PA=
·S△ACD·PA=![]() ·S△PCD·d,
·S△PCD·d,
∴![]() ×
×![]() ×2×2
×2×2![]() ×2=
×2=![]() ×2
×2![]() d,∴d=
d,∴d=![]() ,
,
∴点A到平面PCD的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥底面 ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
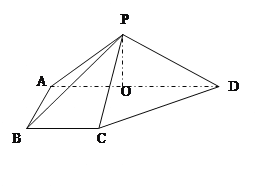
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)线段AD上是否存在点![]() ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与曲线
与曲线![]() 恰有两个不同的交点,记
恰有两个不同的交点,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,
,![]() 是椭圆
是椭圆![]() 上一动点,点
上一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,记
对称,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,若随机从集合
,若随机从集合![]() 中分别抽出一个元素
中分别抽出一个元素![]() ,则
,则![]() 的概率是___.
的概率是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A. 若直线a,b与平面α所成角都是30°,则这两条直线平行
B. 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C. 若直线a,b平行,则这两条直线中至少有一条与平面α平行
D. 若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:(1)对于定义域上的任意
同时满足:(1)对于定义域上的任意![]() ,恒有
,恒有![]() ;(2)对于定义域上的任意
;(2)对于定义域上的任意![]() ,
,![]() ,当
,当![]() 时,恒有,
时,恒有,![]() 则称函数
则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④ ,则被称为“理想数”的有________(填相应的序号).
,则被称为“理想数”的有________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体![]() ,其中四边形
,其中四边形![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,
为矩形, ![]() ,且
,且![]() ,
, ![]() .
.
(1)试判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,请说明理由;
,请说明理由;
(2)若![]() ,求该几何体的表面积.
,求该几何体的表面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() ,射线
,射线![]() 与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A,B两点(异于M).
与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A,B两点(异于M).
(1)求证:直线AB的斜率为定值;
(2)求![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com