
【题目】已知函数f(x)=x2+alnx. (Ⅰ)当a=﹣2时,求函数f(x)的单调区间和极值;
(Ⅱ)若g(x)=f(x)+ ![]() 在[1,+∞)上是单调增函数,求实数a的取值范围.
在[1,+∞)上是单调增函数,求实数a的取值范围.
【答案】解:(Ⅰ)∵函数f(x)=x2+alnx,∴函数f(x)的定义域为(0,+∞). 当a=﹣2时, ![]() =
= ![]() .
.
当x变化时,f′(x)和f(x)的值的变化情况如下表:
x | (0,1) | 1 | (1,+∞) |
f′(x) | ﹣ | 0 | + |
f(x) | 递减 | 极小值 | 递增 |
由上表可知,函数f(x)的单调递减区间是(0,1)、单调递增区间是(1,+∞)、极小值是f(1)=1.
(Ⅱ) 由g(x)=x2+alnx+ ![]() ,得
,得 ![]() .
.
若函数g(x)为[1,+∞)上的单调增函数,则g′(x)≥0在[1,+∞)上恒成立,
即不等式2x﹣ ![]() +
+ ![]() ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立.
也即a≥ ![]() 在[1,+∞)上恒成立.
在[1,+∞)上恒成立.
令φ(x)= ![]() ,则φ′(x)=﹣
,则φ′(x)=﹣ ![]() .
.
当x∈[1,+∞)时,φ′(x)=﹣ ![]() ﹣4x<0,
﹣4x<0,
∴φ(x)= ![]() 在[1,+∞)上为减函数,∴φ(x)max=φ(1)=0.
在[1,+∞)上为减函数,∴φ(x)max=φ(1)=0.
∴a≥0.
∴a的取值范围为[0,+∞)
【解析】(Ⅰ)函数f(x)的定义域为(0,+∞).当a=﹣2时, ![]() =
= ![]() ,由此利用导数性质能求出函数f(x)的单调区间和极值.(Ⅱ) 由g(x)=x2+alnx+
,由此利用导数性质能求出函数f(x)的单调区间和极值.(Ⅱ) 由g(x)=x2+alnx+ ![]() ,得
,得 ![]() ,令φ(x)=
,令φ(x)= ![]() ,则φ′(x)=﹣
,则φ′(x)=﹣ ![]() .由此利用导数性质能求出a的取值范围.
.由此利用导数性质能求出a的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() 叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: 1)函数y=x3﹣x2+1图象上两点A、B的横坐标分别为1,2,则φ(A,B)>
叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: 1)函数y=x3﹣x2+1图象上两点A、B的横坐标分别为1,2,则φ(A,B)> ![]() ;
;
2)存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
3)设点A、B是抛物线,y=x2+1上不同的两点,则φ(A,B)≤2;
4)设曲线y=ex上不同两点A(x1 , y1),B(x2 , y2),且x1﹣x2=1,若tφ(A,B)<1恒成立,则实数t的取值范围是(﹣∞,1);
以上正确命题的序号为(写出所有正确的)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)函数f(x)在x>0时是增函数,x<0时也是增函数,所以f(x)是增函数;
(2)若m=loga2,n=logb2且m>n,则a<b;
(3)函数f(x)=x2+2(a﹣1)x+2在区间(﹣∞,4]上是减函数,则实数a的取值范围是a≤﹣3;
(4)y=log ![]() (x2+x﹣2)的减区间为(1,+∞).
(x2+x﹣2)的减区间为(1,+∞).
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为3m的 ![]() 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 .
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 . 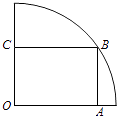
(1)写出体积V关于x的函数关系式,并指出定义域;
(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com