


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年陕西省高三第一次月考文科数学卷 题型:解答题
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:元,
(单位:元,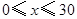 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期期中考试数学文卷 题型:解答题
(本小题满分14分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值 (单位:元,
(单位:元, )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省豫南九校高三上学期第二次联考文科数学卷 题型:解答题
(本小题满分12分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出商品件数与商品单价的降低值x(单位:元,0≤x≤30)的平方成正比,已知商品单价降低2元时,一星期多卖出24件
(1)将一个星期的商品销售利润表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com