
分析 (1)设等比数列{an}的公比为q,由a1+a4=9,a2a3=8.可得$\left\{\begin{array}{l}{{a}_{1}(1+{q}^{3})=9}\\{{a}_{1}^{2}{q}^{3}=8}\end{array}\right.$,解得并利用数列{an}是递增的等比数列即可得出;
(2)由数列{bn}满足$\frac{{a}_{1}}{{b}_{1}}$+$\frac{{a}_{2}}{{b}_{2}}$+…+$\frac{{a}_{n}}{{b}_{n}}$=(n2+n+2)•2n(n∈N*),利用递推关系可得:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{2}^{n-1}}{{b}_{n}}$=(n2+n+2)•2n-[(n-1)2+(n-1)+2]•2n-1,化为:bn=$\frac{1}{{n}^{2}+3n+2}$.可得bn=$\left\{\begin{array}{l}{\frac{1}{8},n=1}\\{\frac{1}{n+1}-\frac{1}{n+2},n≥2}\end{array}\right.$.再利用“裂项求和”即可得出.
解答 解:(1)设等比数列{an}的公比为q,∵a1+a4=9,a2a3=8.
∴$\left\{\begin{array}{l}{{a}_{1}(1+{q}^{3})=9}\\{{a}_{1}^{2}{q}^{3}=8}\end{array}\right.$,解得a1=1,q=2;或a1=8,q=$\frac{1}{2}$.
∵数列{an}是递增的等比数列,∴a1=8,q=$\frac{1}{2}$舍去.
∴a1=1,q=2;
∴an=2n-1.
(2)∵数列{bn}满足$\frac{{a}_{1}}{{b}_{1}}$+$\frac{{a}_{2}}{{b}_{2}}$+…+$\frac{{a}_{n}}{{b}_{n}}$=(n2+n+2)•2n(n∈N*),
∴当n≥2时,$\frac{{a}_{1}}{{b}_{1}}$+$\frac{{a}_{2}}{{b}_{2}}$+…+$\frac{{a}_{n-1}}{{b}_{n-1}}$=[(n-1)2+(n-1)+2]•2n-1,
可得$\frac{{a}_{n}}{{b}_{n}}$=$\frac{{2}^{n-1}}{{b}_{n}}$=(n2+n+2)•2n-[(n-1)2+(n-1)+2]•2n-1,化为:bn=$\frac{1}{{n}^{2}+3n+2}$.
当n=1时,$\frac{{a}_{1}}{{b}_{1}}$=8,∴b1=$\frac{1}{8}$.
∴bn=$\left\{\begin{array}{l}{\frac{1}{8},n=1}\\{\frac{1}{n+1}-\frac{1}{n+2},n≥2}\end{array}\right.$.
∴当n≥2时,数列{bn}的前n项和Sn=$\frac{1}{8}$+$(\frac{1}{3}-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{5})$+…+$(\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{11}{24}$-$\frac{1}{n+2}$.
当n=1时也成立,
∴数列{bn}的前n项和Sn=$\frac{11}{24}$-$\frac{1}{n+2}$.
点评 本题考查了等比数列的通项公式及其单调性、递推关系的应用、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
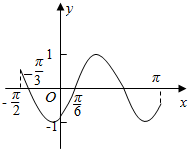 若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )| A. | $ω=2,φ=\frac{π}{3}$ | B. | $ω=2,φ=-\frac{2π}{3}$ | C. | $ω=\frac{1}{2},φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2},φ=-\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
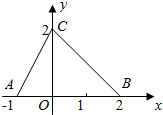 如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )| A. | {x|-1<x≤0} | B. | {x|-1≤x≤1} | C. | {x|-1≤x<1} | D. | {x|-1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=lgx2,g(x)=2lgx | B. | f(x)=1,g(x)=x0 | ||
| C. | $f(x)=\sqrt{x^2},g(x)={(\sqrt{x})^2}$ | D. | $f(x)=x,g(x)={log_a}{a^x}(a>0且a≠1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com