
分析 根据题意可知在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,推断出m≥-1-x恒成立,进而根据x的范围可推知-1-x最大为0,判断出m的范围,进而根据f(x+m)≥f(x),求得(x+m)2≥x2,化简求得m≥-2x恒成立,进而根据x的范围确定-2x的范围,进而求得m的范围.
解答 解:在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,则x+m≥-1恒成立,即m≥-1-x恒成立.
对于x∈[-1,+∞),当x=-1时-1-x最大为0,所以有m≥0.
又因为f(x+m)≥f(x),即(x+m)2≥x2在x∈[-1,+∝)上恒成立,化简得m2+2mx≥0,
又因为m≥0,所以m+2x≥0即m≥-2x恒成立,当x=-1时-2x最大为2,所以m≥2
综上可知m≥2.
故答案为m≥2.
点评 本题主要考查了抽象函数极其应用.考查了学生分析问题和解决问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
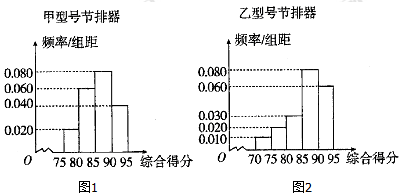
| 综合得分k的范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
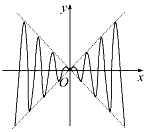 如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )
如图,虚线部分是平面直角坐标系四个象限的角平分线,实线部分是函数y=f(x)的部分图象,则f(x)可能是( )| A. | x2sinx | B. | xsinx | C. | x2cosx | D. | xcosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $1+\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [2,+∞) | C. | (2,$\frac{5}{2}$) | D. | (2,$\frac{10}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0] | B. | (-1,0) | C. | [0,1] | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有极大值,没有极小值 | B. | 没有极大值,有极小值 | ||
| C. | 既有极大值,也有极小值 | D. | 既无极大值,也没有极小值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com