解答:解:(1)∵四边形CFED与ABFE都是正方形
∴EF⊥DE,EF⊥AE,又DE∩EA=E,∴EF⊥平面ADE,---------------(2分)
又∵EF∥AB,∴AB⊥平面ADE
∵AB?平面ABCD,∴平面ABCD⊥平面ADE-------------------------(4分)
(2)证法一:过点M作MM
1⊥BF交BF于M
1,
过点N作NN
1⊥CF交BF于N
1,连结M
1N
1,------------(5分)
∵MM
1∥AB,NN
1∥EF∴MM
1∥NN
1又∵
===,
∴MM
1=NN
1--------------------------------(7分)
∴四边形MNN
1M
1为平行四边形,----------------------(8分)
∴MN∥N
1M
1,又MN?面BCF,N
1M
1?面BCF,∴MN∥面BCF.-(10分)
[法二:过点M作MG⊥EF交EF于G,连结NG,则
==,∴NG∥CF-------------(6分)
又NG?面BCF,CF?面BCF,∴NG∥面BCF,------------(7分)
同理可证得MG∥面BCF,又MG∩NG=G,∴平面MNG∥平面BCF--------(9分)
∵MN?平面MNG,∴MN∥面BCF.--------------------------------------------(10分)]
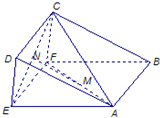
(3)如图将平面EFCD绕EF旋转到与ABFE在同一平面内,则当点
A、P、N在同一直线上时,PA+PN最小,------------------------------------(11分)
在△AEN中,∵
∠AEN=135°,AE=1,NE=由余弦定理得AN
2=AE
2+EN
2-2AE•ENcos135°,------(13分)
∴
AN=,
即
(PA+PN)min=.-----------------------(14分)

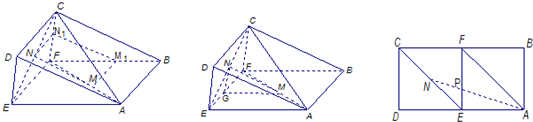
 (2013•揭阳二模)如图,已知三棱柱BCF-ADE的侧面CFED与ABFE都是边长为1的正方形,M、N两点分别在AF和CE上,且AM=EN.
(2013•揭阳二模)如图,已知三棱柱BCF-ADE的侧面CFED与ABFE都是边长为1的正方形,M、N两点分别在AF和CE上,且AM=EN. ∵MM1∥AB,NN1∥EF∴MM1∥NN1
∵MM1∥AB,NN1∥EF∴MM1∥NN1

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案 (2013•揭阳二模)如图所示,C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为
(2013•揭阳二模)如图所示,C,D是半圆周上的两个三等分点,直径AB=4,CE⊥AB,垂足为E,BD与CE相交于点F,则BF的长为