
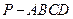
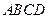
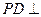
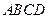
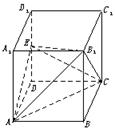
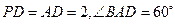 ,
,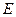 、
、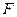 分别为
分别为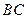 、
、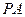 的中点。
的中点。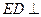 平面
平面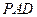 ;
;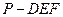 的体积;
的体积;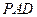 与平面
与平面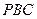 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。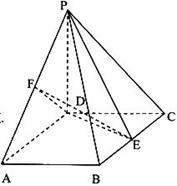
 (3)
(3)

 ,又
,又 ,
, ------------ 2分
------------ 2分 平面
平面 ,
, , ------------3分
, ------------3分 ,
, 平面PAD。 ------------4分
平面PAD。 ------------4分 ,
, , ------5分
, ------5分 --------8分
--------8分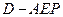 ,
,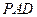 的一个法向量为
的一个法向量为
 ,
,
 ,
,
 得
得 ----------11分
----------11分 --------13分
--------13分 平面PAD与平面PBC所成的锐二面角大小的余弦值为
平面PAD与平面PBC所成的锐二面角大小的余弦值为 -------14分
-------14分 平面
平面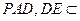 平面
平面 ,
, 平面
平面 平面
平面 -------9分
-------9分
 平面
平面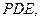 又
又 平面
平面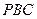
 平面
平面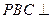 平面
平面 --------10分
--------10分 就是平面
就是平面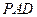 与平面
与平面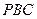 所成二面角的平面角 ---------12分
所成二面角的平面角 ---------12分 在
在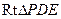 中,
中,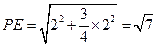
 --------14分
--------14分

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:不详 题型:解答题
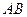 是圆柱体
是圆柱体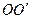 的一条母线,
的一条母线,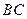 过底面圆的圆心
过底面圆的圆心 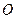 ,
,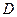 是圆
是圆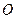 上不与点
上不与点 、
、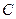 重合的任意一点,已知棱
重合的任意一点,已知棱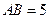 ,
, 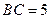 ,
,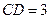 .
.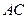 与平面
与平面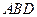 所成的角的大小;
所成的角的大小; 绕母线
绕母线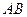 转动一周,求
转动一周,求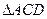 的三边在旋 转过程中所围成的几何体的体积.
的三边在旋 转过程中所围成的几何体的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.27π | B.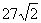 π π |
C.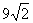 π π | D.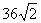 π π |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 与球O有且仅有一公共点P,从直线
与球O有且仅有一公共点P,从直线 出发的两个半平面截球O的两个截面圆O1和圆O2的半径1和2,若这两个半平面
出发的两个半平面截球O的两个截面圆O1和圆O2的半径1和2,若这两个半平面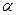 ,
, 所成二面角为1200,则球O的表面积为 。
所成二面角为1200,则球O的表面积为 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com