练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下列命题：

    ①两个平面垂直，过其中一个平面内一点作与它们交线垂直的直线，必垂直于另一个平面；

    ②两个平面垂直，分别在这两个平面内且互相垂直的两直线，一定分别与另一平面垂直；

    ③两平面垂直，分别在这两个平面内的两直线互相垂直.

    其中假命题是_______.

    解析：(1)若该点在两个平面的交线上，则命题是错误的.如下图(甲).正方体AC1中，平面AC⊥平面AD1，平面AC∩平面AD1=AD，在AD上取点A，连结AB1，则AB1⊥AD即过棱上一点A的直线AB1与棱垂直，但AB1与平面ABCD不垂直，其错误的原因是AB1没有保证在平面ADD1A1内，可以看出线在面内这一条件的重要性.

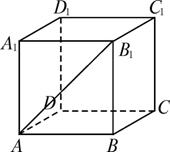
    甲

    (2)该命题注意了直线在平面内，但不能保证这两条直线都与棱垂直，如下图(乙)，在正方体AC1中，平面AD1⊥平面AC，AD1平面ADD1A，AB平面ABCD，且AB⊥AD1即AB与AD1相互垂直，但AD1与平面ABCD不垂直.

    (3)如图乙所示，正方体AC1中，平面ADD1A1⊥平面ABCD，AD1平面ADD1A1，AC平面ABCD，AD1与AC所成的角为60°,即AD1与AC不垂直.

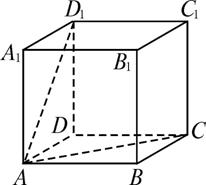
    乙

    答案：①②③

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    有下列命题：
    ①有两个面平行，其余各面都是四边形的几何体叫棱柱；
    ②有两个面平行，其余各面都是平行四边形的几何体叫棱柱； 
    ③有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱；
    ④用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．
    ⑤有一个面是多边形，其余各面都是三角形的几何体是棱锥．
    其中正确的命题的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；
    ②有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥；
    ③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫棱台．
    以上命题中真命题的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列命题：①有两个面平行，其余各面都是四边形的几何体叫棱柱；②有两个面平行，其余各面都是平行四边形的几何体叫棱柱； ③有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱；④用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．其中正确的命题的个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    判断下列命题的真假

    ①两个平面垂直，过其中一个平面内一点作与它们交线垂直的直线，必垂直于另一个平面；

    ②两个平面垂直，分别在这两个平面内且互相垂直的两直线，一定分别与另一平面垂直；

    ③两平面垂直，分别在这两个平面内的两直线互相垂直.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    判断下列命题的真假

    ①两个平面垂直，过其中一个平面内一点作与它们交线垂直的直线，必垂直于另一个平面；

    ②两个平面垂直，分别在这两个平面内且互相垂直的两直线，一定分别与另一平面垂直；

    ③两平面垂直，分别在这两个平面内的两直线互相垂直.

    查看答案和解析>>

    同步练习册答案