
分析 (1)若p∧q为真命题,则命题p,q均为真命题,进而可得实数m的取值范围;
(2)若p∨q为真命题,p∧q为假命题,则p,q一真一假,进而可得实数m的取值范围.
解答 解:∵${x^2}+{y^2}-2x-4y+\frac{19}{4}=0$,∴${({x-1})^2}+{({y-2})^2}=\frac{1}{4}$,
所以该圆的圆心为(1,2),半径为$\frac{1}{2}$,圆心到直线的距离$d=\frac{{|{m-2+2}|}}{{\sqrt{1+{m^2}}}}=\frac{|m|}{{\sqrt{1+{m^2}}}}$.
若p为真,则圆心到直线的距离小于半径,即$\frac{|m|}{{\sqrt{1+{m^2}}}}<\frac{1}{2}$,解得$-\frac{{\sqrt{3}}}{3}<m<\frac{{\sqrt{3}}}{3}$.
若q为真,则$m≥2sin({2x+\frac{π}{6}})+2cos2x$在$[{-\frac{π}{6},\frac{π}{4}}]$上有解,
因为$2sin({2x+\frac{π}{6}})+2cos2x=2sin2xcos\frac{π}{6}+2cos2xsin\frac{π}{6}+2cos2x=\sqrt{3}sin2x+3cos2x=2\sqrt{3}sin({2x+\frac{π}{3}})$,又由$x∈[{-\frac{π}{6},\frac{π}{4}}]$,得$0≤2x+\frac{π}{3}≤\frac{5π}{6}$,
所以$0≤2\sqrt{3}sin({2x+\frac{π}{3}})≤2\sqrt{3}$,
即$0≤2sin({2x+\frac{π}{6}})+2cos2x≤2\sqrt{3}$,故若q为真,则m≥0…(6分)
(1)若p∧q为真,则应满足$\left\{{\begin{array}{l}{-\frac{{\sqrt{3}}}{3}<m<\frac{{\sqrt{3}}}{3}}\\{m≥0}\end{array}}\right.$,即$0≤m<\frac{{\sqrt{3}}}{3}$,
故实数m的取值范围为$[{0,\frac{{\sqrt{3}}}{3}})$…(8分)
(2)若p∧q为真命题,p∧q为假命题,则p,q一真一假,
若p真q假,则应满足$\left\{{\begin{array}{l}{-\frac{{\sqrt{3}}}{3}<m<\frac{{\sqrt{3}}}{3},即-\frac{{\sqrt{3}}}{3}<m<0}\\{m<0}\end{array}}\right.$,
若p假q真,则应满足$\left\{{\begin{array}{l}{m≤-\frac{{\sqrt{3}}}{3}或m≥\frac{{\sqrt{3}}}{3},即m≥\frac{{\sqrt{3}}}{3}}\\{m≥0}\end{array}}\right.$
综上所述,实数m的取值范围为$({-\frac{{\sqrt{3}}}{3},0})∪[{\frac{{\sqrt{3}}}{3},+∞})$…(12分)
点评 本题以命题的真假判断与应用为载体,考查了直线与圆的位置关系,三角函数的图象和性质,复合命题等知识点,难度中档.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=$\frac{π}{4}$,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=$\frac{π}{4}$,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
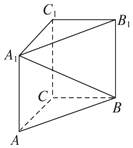 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | $\frac{{\sqrt{6}}}{5}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{100}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{25}-\frac{y^2}{100}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
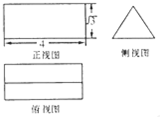 一个正棱柱(底面是正三角形、侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的表面积等于( )
一个正棱柱(底面是正三角形、侧棱垂直于底面的棱柱)的三视图如图所示,则该三棱柱的表面积等于( )| A. | 2$\sqrt{3}$+12 | B. | 2$\sqrt{3}$+24 | C. | 2$\sqrt{3}$+12 | D. | 6$\sqrt{3}$+24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
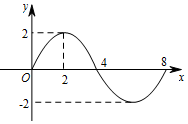 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )| A. | $\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com