
【题目】已知函数![]() ,函数
,函数![]() 是奇函数.
是奇函数.
(1)判断函数![]() 的奇偶性,并求实数
的奇偶性,并求实数![]() 的值;
的值;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某城市出租车的收费标准是:3千米以内(含3千米),收起步价8元;3千米以上至8千米以内(含8千米),超出3千米的部分按![]() 元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米时应付的车费;
(2)试写出车费![]() (元)与里程
(元)与里程![]() (千米)之间的函数解析式并画出图像;
(千米)之间的函数解析式并画出图像;

(3)小陈周末外出,行程为10千米,他设计了两种方案:
方案1:分两段乘车,先乘一辆行驶5千米,下车换乘另一辆车再行5千米至目的地
方案2:只乘一辆车至目的地,试问:以上哪种方案更省钱,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市自来水公司每两个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过![]() 吨时,按每吨
吨时,按每吨![]() 元收取;当该用户用水量超过
元收取;当该用户用水量超过![]() 吨时,超出部分按每吨
吨时,超出部分按每吨![]() 元收取.
元收取.
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为![]() 元,且甲、乙两用户用水量之比为
元,且甲、乙两用户用水量之比为![]() ,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
,试求出甲、乙两用户在该收费周期内各自的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,空气质量成为人们越来越关注的话题,空气质量指数(,Air Quality Inder简称 ![]() )是定量描述空气质量状况的指数,空气质量按照
)是定量描述空气质量状况的指数,空气质量按照 ![]() 大小分为六级,
大小分为六级, ![]() 为优;
为优; ![]() 为良;
为良; ![]() 为轻度污染;
为轻度污染; ![]() 为中度污染;
为中度污染; ![]() 为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的
为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的 ![]() 的茎叶图如下:
的茎叶图如下: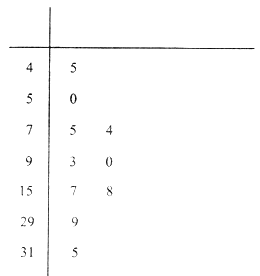
(1)利用该样本估计该地本月空气质量优良( ![]() )的天数;(按这个月总共30天计算)
)的天数;(按这个月总共30天计算)
(2)现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究,求抽取的2天中至少有一天空气质量是优的概率;
(3)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为 ![]() ,求
,求 ![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)若函数F(x)= ![]() +ax2在
+ax2在 ![]() 上为减函数,求
上为减函数,求 ![]() 的取值范围;
的取值范围;
(2)当 ![]() 时,
时, ![]() ,当
,当 ![]() 时,方程
时,方程 ![]() -
- ![]() =0有两个不等的实根,求实数
=0有两个不等的实根,求实数 ![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax2+2(a﹣3)x+1在区间[﹣2,+∞)上递减,则实数a的取值范围是( )
A.(﹣∞,0)
B.[﹣3,+∞)
C.[﹣3,0]
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
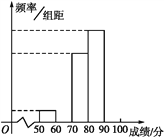
【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
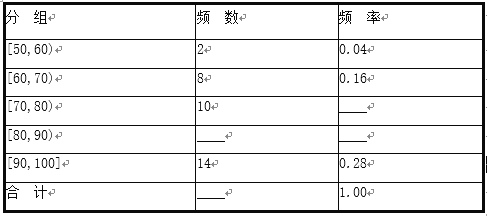
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级学生成绩的中位数;
(3)如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com