
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2若函数![]() 有两个零点分别记为
有两个零点分别记为![]() .
.
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
【答案】⑴见解析;⑵见解析;⑶见证明
【解析】
(1)![]() ,可分
,可分![]() 四种情况讨论
四种情况讨论![]() 的符号后可得
的符号后可得![]() 的单调性.
的单调性.
(2)①结合(1)中函数的单调性讨论,当![]() 时,
时,![]() 无两个零点,当
无两个零点,当![]() 时,利用零点存在定理可得
时,利用零点存在定理可得![]() 有两个不同的零点,当
有两个不同的零点,当![]() 时,利用
时,利用![]() 时
时![]() 恒成立得到
恒成立得到![]() 在
在![]() 上没有零点,当
上没有零点,当![]() 时,结合函数的单调性及
时,结合函数的单调性及![]() 可得
可得![]() 在
在![]() 上不可能有两个零点.
上不可能有两个零点.
②结合函数的导数可知原不等式的证明可归结为![]() ,构建新函数
,构建新函数![]() ,利用导数可证
,利用导数可证![]() 在
在![]() 上为单调增函数,设
上为单调增函数,设![]() ,利用
,利用![]() 及
及![]() 可得
可得![]() .
.
(1)![]() ,
,
(i)当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增.
单调递增.
(ii)当![]() 时,
时,
![]() 时,
时,![]() 单调递增;
单调递增;
![]() 时,
时,![]() 单调递减;
单调递减;
![]() 时,
时,![]() 单调递增.
单调递增.
(iii)当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单增.
上单增.
(iv)当![]() 时,
时,
![]() 时,
时,![]() 单调递增;
单调递增;
![]() 时,
时,![]() 单调递减,
单调递减,
![]() 时,
时,![]() 单调递增.
单调递增.
综上所述:![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增.
上单调递增.
(2)①![]() ,
,
(i)当![]() 时,
时,![]() ,只有一个零点,舍去;
,只有一个零点,舍去;
(ii)当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
![]()
又![]() ,取
,取![]() 且
且![]() ,
,
则![]()
![]()
![]()
![]() ,
,
![]() 存在两个零点.
存在两个零点.
(iii)当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 时,
时,![]()
![]() 不可能有两个零点,舍去.
不可能有两个零点,舍去.
(iv)当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 不可能有两个零点,舍去.
不可能有两个零点,舍去.
(v)当![]() 时,
时,![]() 时,
时,![]() ,又
,又![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,因
上单调递增,因![]() ,
,![]() 不可能有两个零点,舍去.
不可能有两个零点,舍去.
综上所述:![]() .
.
②由①知:![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
要证![]() , 即证
, 即证![]() ,即证
,即证![]() ,
,
令![]() ,则
,则
![]()
![]()
![]()
当![]() 时,
时,![]() 单调递增.
单调递增.
不妨设![]() ,则
,则![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,
,![]() ,原命题得证.
,原命题得证.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() 的动点,设直线
的动点,设直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)当椭圆![]() 内切于圆
内切于圆![]() 时,设动直线
时,设动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,问:
,问:![]() 的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.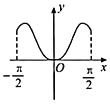
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值点;
的极值点;
(2)定义:若函数![]() 的图像与直线
的图像与直线![]() 有公共点,我们称函数
有公共点,我们称函数![]() 有不动点.这里取:
有不动点.这里取:![]() ,若
,若![]() ,如果函数
,如果函数![]() 存在不动点,求实数
存在不动点,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点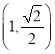 ,且椭圆的离心率为
,且椭圆的离心率为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中垂线交椭圆
的中垂线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
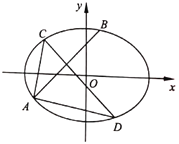
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 长的最大值;
长的最大值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() ,
,![]() 在边
在边![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都与平面
都与平面![]() 垂直,如图(2).
垂直,如图(2).

(1)试判断图(2)中直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求平面![]() 和平面
和平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com