
【题目】下列说法正确的个数是( )
①“x>1”是“x>2”的充分不必要条件;
②f(x)是其定义域上的可导函数,“f'(x0)=0”是“y=f(x)在x0处有极值”的充要条件;
③命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;
④若“p且q”为假命题,则p、q均为假命题.
A.1B.2C.3D.4
【答案】A
【解析】
利用充要条件判断①;函数的极值的概念判断②;否命题概念判断③;复合命题的真假判断④.
解:①“x>2”“x>1”,反之不成立,所以“x>1”是“x>2”的必要不充分条件,①错;
②f(x)是其定义域上的可导函数,“f'(x0)=0”不能说明“y=f(x)在x0处有极值”,如![]() ,
,![]() ,但0不是极值点,反之成立,所以f(x)是其定义域上的可导函数,“f'(x0)=0”是“y=f(x)在x0处有极值”的必要条件,②错;
,但0不是极值点,反之成立,所以f(x)是其定义域上的可导函数,“f'(x0)=0”是“y=f(x)在x0处有极值”的必要条件,②错;
③命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;满足否命题的条件,③正确;
④若“p且q”为假命题,则p、q至少一个是假命题,所以原判断不成立,④错.
故选:A.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】向体积为1的正方体密闭容器内注入体积为![]() 的液体,旋转容器,下列说法正确的是( )
的液体,旋转容器,下列说法正确的是( )
A.当![]() 时,容器被液面分割而成的两个几何体完全相同
时,容器被液面分割而成的两个几何体完全相同
B.![]() ,液面都可以成正三角形形状
,液面都可以成正三角形形状
C.当液面与正方体的某条体对角线垂直时,液面面积的最大值为![]()
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,下图是某省近五年进出口情况统计图,下列描述正确的是( )
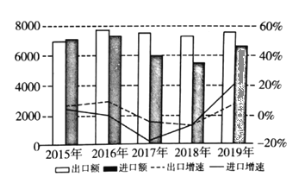
A.这五年,2015年出口额最少B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降D.这五年,2019年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本4元,且以9元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂.根据以往100天的资料统计,得到如表需求量表:
需求量/个 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天数 | 15 | 25 | 30 | 20 | 10 |
该蛋糕店一天制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(1)当x=135时,若X=130时获得的利润为T1,X=140时获得的利润为T2,试比较T1和T2的大小;
(2)当X=130时,根据上表,从利润T不少于560元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润T关于市场需求量x的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为ξ,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计π的值,先请240名同学,每人随机写下两个都小于1的正实数x,y组成的实数对(x,y);若将(x,y)看作一个点,再统计点(x,y)在圆x2+y2=1外的个数m;最后再根据统计数m来估计π的值,假如统计结果是m=52,那么可以估计π的近似值为_______.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
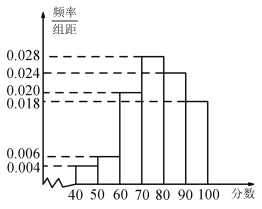
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com