Question

在数列a_n中，若a₁,a₂ 是正整数，且a_n=|a _n-1-a _n-2|,n=3，4，5，…，则称|a_n|为“绝对差数列”.

（1）举出一个前五项不为零的“绝对差数列”（只要求写出前十项）；

（2）若“绝对差数列”|a_n|中，a₂₀=3,a₂₁=0,数列|b_n|满足b_n=a_n+a _n+1+a _n+2,n=1，2，3，…，分别判断当n→∞时, a_n与b_n的极限是否存在，如果存在，求出其极限值；

（3）证明：任何“绝对差数列”中总含有无穷多个为零的项.

Answer 1

解:（1）a₁=3,a₂=1,a₃=2,a₄=1,a₅=1,a₆=0,a₇=1,a₈=1,a₉=0,a₁₀=1.（答案不唯一）

（2）因为在绝对差数列{a_n}中，a₂₀=3,a₂₁=0.所以自第20 项开始，该数列是a₂₀=3,a₂₁=0,a₂₂=3,a₂₃=3,a₂₄=0,a₂₅=3,a₂₆=3,a₂₇=0,…

即自第 20项开始.每三个相邻的项周期的取值 3，0，3.所以当n→∞时，a_n的极限不存在.

当n≥20时,b_n=a_n+a _n+1+a _n+2=6,所以.

（3）证明：根据定义，数列{a_n}必在有限项后出现零项.证明如下：

假设{a_n}中没有零项，由于a_n=|a _n-1-a _n-2|,所以对于任意的n，都有a_n≥1,从而当a _n-1＞a _n-2时,a_n=a_n-1-a _n-2≤a _n-1-1(n≥3);

当a _n-1＜a _n-2时，a_n= a _n-2-a _n-1≤a _n-2-1(n≥3)；

即a_n的值要么比a _n-1至少小1，要么比a _n-2至少小1.

令C_n=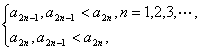

则0＜C_A≤C_n-1-1(n=2,3,4,…)

由于C₁是确定的正整数,这样减少下去必然存在某项C₁＜0,这与C_n＞0(n=1,2,3,…,)矛盾,从而{a_n}必有零项.

若第一次出现的零项为第n项,记a_n-1=A(A≠0),则自第n项开始,每三个相邻的项周期地取值0,A,A,即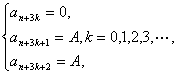

所以绝对差数列{a_n}中有无穷多个零的项.