
分析 由点到直线的距离得a-b=2或a-b=-2,把P(a,b)代入双曲线方程,求出a,b,即可求出|a+b|的值.
解答 解:∵双曲线$\frac{{x}^{2}}{4}$-y2=1上一点P(a,b)到直线y=x的距离为$\sqrt{2}$,
∴由点到直线的距离得a-b=2或a-b=-2,
把P(a,b)代入双曲线方程,得$\frac{{a}^{2}}{4}$-b2=1,
(a+2b)(a-2b)=4,
当a-b=2时,上式化为:(3b+2)(2-b)=4,b≠0解得b=$\frac{4}{3}$,|a+b|=|2b+2|=$\frac{11}{3}$.
当a-b=-2时,上式化为:(3b-2)(-2-b)=4,解得b=$±2\sqrt{2}$.
|a+b|=|2b-2|=4$\sqrt{2}±2$.
点评 本题考查双曲线的简单性质的应用,是中档题,解题时要注意点到直线的距离公式的应用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | -30 | C. | ±30 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
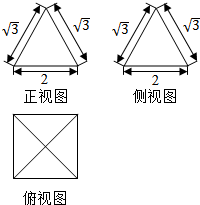
| A. | $4\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 4$\sqrt{2}$+4 | D. | 4$\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
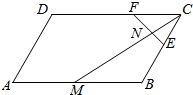 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )| A. | $\frac{15}{14}$ | B. | 1 | C. | $\frac{5}{14}$ | D. | -$\frac{5}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -$\frac{1}{4}$ | C. | -4或-$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com