
【题目】直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2, ![]() =λ
=λ ![]() .
. 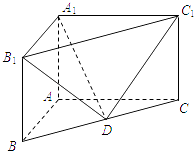
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1﹣A1C1﹣D的大小为60°,求实数λ的值.
【答案】
(1)解:分别以AB,AC,AA1所在直线为x,y,z轴,建立空间直角坐标系.
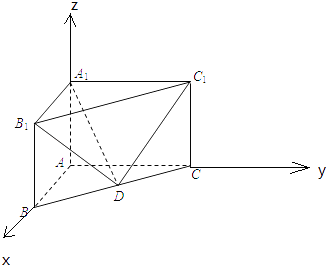
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,2),B1(2,0,2),C1(0,4,2),
当λ=1时,D为BC的中点,∴D(1,2,0),
![]() =(1,﹣2,2),
=(1,﹣2,2), ![]() =(0,4,0),
=(0,4,0), ![]() =(1,2,﹣2),
=(1,2,﹣2),
设平面A1C1D的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 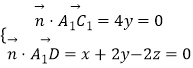 ,取x=2,
,取x=2,
得 ![]() =(2,0,1),
=(2,0,1),
又cos< ![]() >=
>= 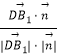 =
= ![]() =
= ![]() ,
,
∴直线DB1与平面A1C1D所成角的正弦值为 ![]() .)
.)
(2)解:∵ ![]() =
= ![]() ,∴D(
,∴D( ![]() ,
, ![]() ,0),
,0),
∴ ![]() =(0,4,0),
=(0,4,0), ![]() =(
=( ![]() ,
, ![]() ,﹣2),
,﹣2),
设平面A1C1D的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 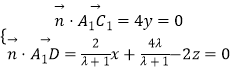 ,取z=1,得
,取z=1,得 ![]() =(λ+1,0,1).
=(λ+1,0,1).
又平面A1B1C1的一个法向量为 ![]() =(0,0,1),
=(0,0,1),
∵二面角B1﹣A1C1﹣D的大小为60°,
∴|cos< ![]() >|=|
>|=| ![]() |=
|= ![]() =
= ![]() ,
,
解得 ![]() 或
或 ![]() (不合题意,舍去),
(不合题意,舍去),
∴实数λ的值为 ![]() .
.
【解析】(1)分别以AB,AC,AA1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线DB1与平面A1C1D所成角的正弦值.(2)求出平面A1C1D的法向量和平面A1B1C1的一个法向量,利用向量法能求出实数λ的值.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则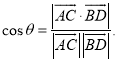 .
.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求证:函数f(x)在实数集R上为增函数;
(2)设g(x)=log2f(x),若关于x的方程g(x)=a有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A,B,C三种商品有购买意向.已知该网民购买A种商品的概率为 ![]() ,购买B种商品的槪率为
,购买B种商品的槪率为 ![]() ,购买C种商品的概率为
,购买C种商品的概率为 ![]() .假设该网民是否购买这三种商品相互独立
.假设该网民是否购买这三种商品相互独立
(1)求该网民至少购买2种商品的概率;
(2)用随机变量η表示该网民购买商品的种数,求η的槪率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数:①f(x)=3|x| , ②f(x)=x3 , ③f(x)=ln ![]() ,④f(x)=
,④f(x)= ![]() ,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证: 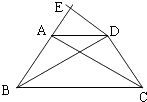
(1)△ABC≌△DCB;
(2)DEDC=AEBD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com