
| A. | (1,+∞) | B. | (e,+∞) | C. | (-∞,-1) | D. | (-∞,-e) |
分析 求出f(-x)的解析式,根据x的范围不同得出两个不同的方程,由两个方程的关系得出f(-x)=f(x)在(0,+∞)上有解,根据函数图象和导数的几何意义得出a的范围
解答  解:∵f(x)=$\left\{\begin{array}{l}{e^x},x≥0\\ ax,x<0\end{array}$,
解:∵f(x)=$\left\{\begin{array}{l}{e^x},x≥0\\ ax,x<0\end{array}$,
∴f(-x)=$\left\{\begin{array}{l}{-ax,x>0}\\{1,x=0}\\{{e}^{-x},x<0}\end{array}\right.$,
显然x=0是方程f(-x)=f(x)的一个根,
当x>0时,ex=-ax①,
当x<0时,e-x=ax②,
显然,若x0为方程①的解,则-x0为方程为②的解,
∵方程f(-x)=f(x)有5个不同的根,
∴方程①在(0,+∞)上有两解,
做出y=ex(x>0)和y=-ax(x>0)的函数图象,如图所示,
设y=kx与y=ex相切,切点为(x0,y0),则$\left\{\begin{array}{l}{{e}^{{x}_{0}}=k}\\{k{x}_{0}={e}^{{x}_{0}}}\end{array}\right.$,解得x0=1,k=e,
∵y=ex与y=-ax在(0,+∞)上有两个交点,
∴-a>e,即a<-e,
故选:D
点评 本题主要考查了函数的解析式,以及函数与方程和根的存在性和根的个数的判断,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | $\sqrt{17}-1$ | D. | $\sqrt{15}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期函数,最小正周期为π | B. | 周期函数,最小正周期为$\frac{π}{2}$ | ||
| C. | 周期函数,最小正周期为2π | D. | 非周期函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
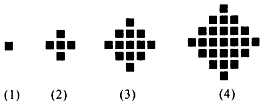 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=sin(2x+\frac{π}{3})$ | C. | $y=sin(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{20}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com