
分析 根据题意,由函数在(0,+∞)上单调递增,且($\frac{1}{2}$)=0,分析可得0<x<$\frac{1}{2}$时,f(x)<0,当x>$\frac{1}{2}$时,f(x)>0,进而结合函数的奇偶性可得当-$\frac{1}{2}$<x<0时,f(x)>0,当x<-$\frac{1}{2}$时,f(x)<0,综合可得f(x)<0的解集,又由f(cosA)<0,可得cosA<-$\frac{1}{2}$或0<cosA<$\frac{1}{2}$,解可得A的范围,即可得答案.
解答 解:根据题意,f(x)在区间(0,+∞)上单调递增,且($\frac{1}{2}$)=0,
则有当0<x<$\frac{1}{2}$时,f(x)<0,当x>$\frac{1}{2}$时,f(x)>0,
又由f(x)是定义在R上的奇函数,则有当-$\frac{1}{2}$<x<0时,f(x)>0,当x<-$\frac{1}{2}$时,f(x)<0,
综合可得当x<-$\frac{1}{2}$或0<x<$\frac{1}{2}$时,f(x)<0,
又由△ABC的内角A满足f(cosA)<0,
则有cosA<-$\frac{1}{2}$或0<cosA<$\frac{1}{2}$,
解可得$\frac{π}{3}$<A<$\frac{π}{2}$或$\frac{2π}{3}$<A<π;
即A∈($\frac{π}{3}$,$\frac{π}{2}$)∪($\frac{2π}{3}$,π);
故答案为:($\frac{π}{3}$,$\frac{π}{2}$)∪($\frac{2π}{3}$,π).
点评 本题考查函数奇偶性与单调性的应用,关键是依据题意,分析得到f(x)<0的解集.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,+∞) | C. | (1,$\sqrt{5}$] | D. | [$\sqrt{5}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
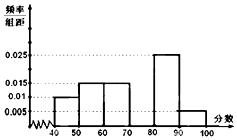 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
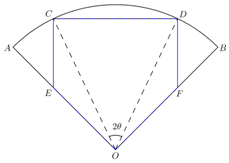 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{27}$ | D. | $\frac{12}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com