设直线
x=
t与函数
f(
x)=
x2,
g(
x)=ln
x的图象分别交于点
M,
N,则当|
MN|达到最小时
t的值为 ( ).
|
MN|=
y=
t2-ln
t(
t>0),
y′=2
t-

=
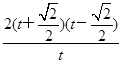
.
当0<
t<
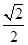
时,
y′<0;当
t>
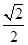
时,
y′>0.
∴
y在
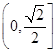
上递减,
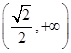
上递增,
∴
t=
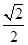
时,|
MN|取得最小值.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
函数
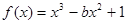
有且仅有两个不同的零点,则
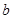
的值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列函数中,
x=0是其极值点的是 ( ).
| A.y=-x3 | B.y=cos2x |
| C.y=tan x-x | D.y=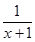 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
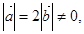
且关于
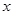
的函数
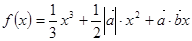
在
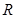
上有极值,则
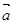
与
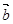
的夹角范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
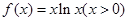
最小值是___________.
查看答案和解析>>

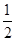
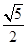
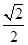
 名校课堂系列答案
名校课堂系列答案