
����Ŀ����ͼ1��һ�����������ε��ܱ������ײ���Ƕ��ͬ����������ʵ��װ�ο飬������ʢ��![]() ��ˮʱ��ˮ��ǡ�þ����������Ķ���P��������������ã�ˮ��Ҳǡ�ù���
��ˮʱ��ˮ��ǡ�þ����������Ķ���P��������������ã�ˮ��Ҳǡ�ù���![]() ��ͼ2�����������ĸ����⣺
��ͼ2�����������ĸ����⣺
A���������ĸߵ������������ߵ�һ�� |
B������������ˮƽ����ʱ��ˮ��Ҳǡ�ù��� |
C������ڷŸ���������ˮ�澲ֹʱ��ˮ�涼ǡ�þ����� |
D��������������ע�� |
����������Ĵ����ǣ� ��д������������Ĵ��ţ���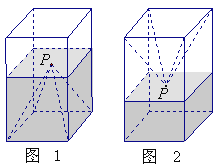
���𰸡�BD
��������
��ͼ��1��ˮ�ĸ߶�h2������ĸ�Ϊh1
ͼ��2����ˮ�����Ϊb2h1-b2h2=b2��h1-h2����
����![]() b2h2=b2��h1-h2��������h1=
b2h2=b2��h1-h2��������h1=![]() h2����A����D��ȷ��
h2����A����D��ȷ��
����B������������ˮƽ����ʱ��P���ڳ������н����ϣ�
��ˮռ�����ڿռ��һ�룬����ˮ��Ҳǡ�þ���P�㣬��B��ȷ��
����C������C��ȷ����ˮ������������һ�������غ�ʱ��
�������ˮ�����Ϊ![]() b2h2��
b2h2��![]() b2h2��ì�ܣ���C����ȷ����ѡBD
b2h2��ì�ܣ���C����ȷ����ѡBD



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() �ĵ���߳�Ϊ2������
�ĵ���߳�Ϊ2������![]() Ϊ�ϵ���
Ϊ�ϵ���![]() �ϵĶ��㣬���������ĸ����ۣ�
�ϵĶ��㣬���������ĸ����ۣ�
����PD=3��������������P������ֻ��һ����
����![]() �����P�Ĺ켣��һ��Բ����
�����P�Ĺ켣��һ��Բ����
����PD��ƽ��![]() ����DP������СֵΪ2��
����DP������СֵΪ2��
����PD��ƽ��![]() ����
����![]() ����ƽ��BDP����������
����ƽ��BDP����������![]() �����������ͼ�ε����Ϊ
�����������ͼ�ε����Ϊ![]() ��
��
����������ȷ���۵����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ӧ����ˮ��ɽ���ǽ�ɽ��ɽ���ĺ��٣�������˵Ľ��������ɡ���̬ˮ����ɫС�������з��֣�ij��ϡˮ�����ĵ������![]() ����λ��ǧ�ˣ���ʩ�÷���
����λ��ǧ�ˣ���ʩ�÷���![]() ����λ��ǧ�ˣ��������¹�ϵ��
����λ��ǧ�ˣ��������¹�ϵ�� �����ϳɱ�Ͷ��Ϊ
�����ϳɱ�Ͷ��Ϊ![]() Ԫ�������ɱ�Ͷ�루������������ʩ�ʵ��˹��ѣ�
Ԫ�������ɱ�Ͷ�루������������ʩ�ʵ��˹��ѣ�![]() Ԫ����֪����ˮ�����г��ۼ۴�ԼΪ15Ԫ��ǧ�ˣ�����·��ͨ����Ӧ�Ǹ�ˮ�����ĵ�������Ϊ
Ԫ����֪����ˮ�����г��ۼ۴�ԼΪ15Ԫ��ǧ�ˣ�����·��ͨ����Ӧ�Ǹ�ˮ�����ĵ�������Ϊ![]() ����λ��Ԫ����
����λ��Ԫ����
������![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
����ʩ�÷���Ϊ����ǧ��ʱ����ˮ�����ĵ����������?��������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�⽨һ���Ȼ�����״�Ļ�̳(��ͼ��ʾ)�����Ȼ��������Ե�![]() ΪԲ�ĵ�����ͬ��Բ�����ӳ���ͨ����
ΪԲ�ĵ�����ͬ��Բ�����ӳ���ͨ����![]() ������ֱ�߶�Χ�ɣ������Ҫ���Ȼ�����ܳ�Ϊ30�ף����д�Բ������Բ�İ뾶Ϊ10��.��СԲ������Բ�İ뾶Ϊ
������ֱ�߶�Χ�ɣ������Ҫ���Ȼ�����ܳ�Ϊ30�ף����д�Բ������Բ�İ뾶Ϊ10��.��СԲ������Բ�İ뾶Ϊ![]() �ף�Բ�Ľ�Ϊ
�ף�Բ�Ľ�Ϊ![]() �����ȣ���
�����ȣ���
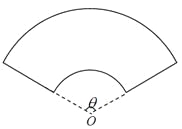
��1����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����֪�ڻ�̳�ı�Ե(ʵ�߲���)����װ��ʱ��ֱ�߲��ֵ�װ�η���Ϊ4Ԫ/�ף����߲��ֵ�װ�η���Ϊ9Ԫ/�ף��軨̳�������װ���ܷ��õı�Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]() ȡ�����ֵ��
ȡ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1������![]() ��ֵ��ĸ�����
��ֵ��ĸ�����
��2����![]() ������ʽ
������ʽ![]() ���������
���������![]() Ϊ����ʱ����
Ϊ����ʱ����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֤�� ![]() .
.
��2��ijͬѧ��һ���о���ѧϰ�з��֣��������ʽ�ӵ�ֵ������ͬһ��������
sin213����cos217����sin13��cos17����
sin215����cos215����sin15��cos15����
sin218����cos212����sin18��cos12����
sin2(��18��)��cos248����sin(��18��)cos48����
sin2(��25��)��cos255����sin(��25��)cos55��.
���Դ��������ʽ����ѡ��һ����������������
���������ļ�����������ͬѧ�ķ����ƹ�Ϊ���Ǻ��ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��ֱ��
��ֱ��![]() .
.
��1����֤����![]() ֱ��
ֱ��![]() ��Բ
��Բ![]() ����������ͬ�Ľ��㣻
����������ͬ�Ľ��㣻
��2���Ƿ����ʵ��![]() ��ʹ��Բ
��ʹ��Բ![]() �����ĸ��㵽ֱ��
�����ĸ��㵽ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �������ڣ����
�������ڣ����![]() �ķ�Χ���������ڣ�˵������.
�ķ�Χ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ƣ�㾭���м��أ�һ���ж�ʮ�ĸ�������ÿ�������У�gui����������ͬ�����ǰ�����Ӱ�ⶨʱ�̵��������г������ⶨ��Ӱ�ӵij��ȣ���ʮ�Ľ������г��仯��ͼ��ʾ���������������г��仯����ͬ���ܶ���ʼ���������г����һ��������磬�����г������һ����磬��һ�ɵ���10�ߣ�һ�ߵ���10�磩������ֽ������г��ǣ� ��
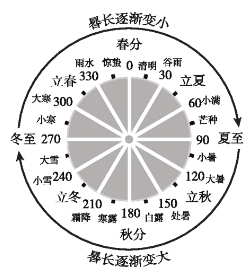
A.�߳����B.�������C.������D.�ij����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() �������ڵ㣨0��3����Բ���ھ����㣨2��1����㣨��2����3����ֱ��
�������ڵ㣨0��3����Բ���ھ����㣨2��1����㣨��2����3����ֱ��![]() �ϣ�
�ϣ�
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2��Բ![]() ��Բ
��Բ![]() ��
��![]() �ཻ��M��N���㣬����Բ�Ĺ�����MN�ij���
�ཻ��M��N���㣬����Բ�Ĺ�����MN�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com