
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( ) 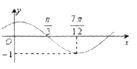
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
【答案】C
【解析】解:由函数的图象可知函数的周期为:T=4×( ![]() ﹣
﹣ ![]() )=π, 所以:ω=
)=π, 所以:ω= ![]() =2,
=2,
因为:图象经过( ![]() ,0),
,0),
所以:0=sin(2× ![]() +φ),可得:2×
+φ),可得:2× ![]() +φ=kπ,k∈Z,
+φ=kπ,k∈Z,
因为:|φ|< ![]() ,
,
所以:φ= ![]() ,可得:f(x)=sin(2x+
,可得:f(x)=sin(2x+ ![]() )=sin[2(x+
)=sin[2(x+ ![]() )],
)],
所以:将f(x)的图象向右平移 ![]() 个单位长度即可得到g(x)=sin2x的图象,
个单位长度即可得到g(x)=sin2x的图象,
故选:C.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水果树的产量![]() (单位:百千克)与肥料费用(单位:百元)满足如下关系:
(单位:百千克)与肥料费用(单位:百元)满足如下关系:  .此外,还需要投入其它成本(如施肥的人工费等)
.此外,还需要投入其它成本(如施肥的人工费等)![]() 百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为
百元.已知这种水果的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水果树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求![]() 的函数关系式;
的函数关系式;
当投入的肥料费用为多少时,该水果树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2009年至2015年生活垃圾无害化处理量(单位:亿吨)的折线图.
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() yi=9.32,
yi=9.32, ![]() tiyi=40.17,
tiyi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 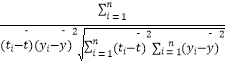 =
= 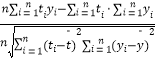
回归方程 ![]() =
= ![]() +
+ ![]() t中斜率和截距的最小二乘估计公式分别为:
t中斜率和截距的最小二乘估计公式分别为: ![]() =
= 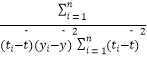 ,
, ![]() =
= ![]() ﹣
﹣ ![]() t.
t.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() …是然对数底数.
…是然对数底数.
(1)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
, ![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求使不等式
时,求使不等式![]() 在一切实数上恒成立的最大正整数
在一切实数上恒成立的最大正整数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com